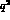 -slope at
-slope at 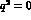 , known as the slope
parameter
, known as the slope
parameter 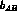 , is defined through
, is defined through
To get an idea of the spatial dimensions of (and charge distribution
inside) strictly neutral hadrons,
one has to extend the above considerations from elastic to transition
form factors. Their 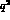 -slope at
-slope at 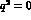 , known as the slope
parameter
, known as the slope
parameter 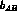 , is defined through
, is defined through
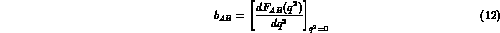
Quite frequently, it is expressed in terms of a parameter
 , having
mass-dimensions and verifying
, having
mass-dimensions and verifying 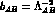 . The
slope parameter
has essentially the same meaning
as in the previous case of charge radii, apart from the factor of 6 in
the definition.
. The
slope parameter
has essentially the same meaning
as in the previous case of charge radii, apart from the factor of 6 in
the definition.
Slope parameters for the 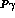 transition form factors, with
transition form factors, with 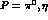 and
and  , have been measured (
, have been measured (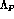 in the
in the 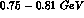 range or, equivalently,
range or, equivalently, 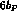 in the
in the 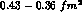 range) indicating that their dimensions are quite
compatible (once one accounts for the factor of 6) with those
previously discussed for their SU(3)-partners. In both cases, one
measures the spatial region where the electromagnetically active
hadron constituents can be found. In the first, charge-radius case one
has to deal with electrostatic or Coulombic interactions, while, in the
later
range) indicating that their dimensions are quite
compatible (once one accounts for the factor of 6) with those
previously discussed for their SU(3)-partners. In both cases, one
measures the spatial region where the electromagnetically active
hadron constituents can be found. In the first, charge-radius case one
has to deal with electrostatic or Coulombic interactions, while, in the
later 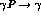 transitions, magnetic interactions are
involved with quark-spin flipping and
transitions, magnetic interactions are
involved with quark-spin flipping and 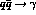 annihilations.
annihilations.