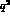 -dependence of
-dependence of 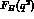 is again related to
the hadron structure, and mean squared-radii can be defined in
anology with eq.(10), i.e.,
is again related to
the hadron structure, and mean squared-radii can be defined in
anology with eq.(10), i.e.,
The essential physical point of the previous discussion can be
extended to the case of relativistic field theories and to different
form factors. The 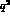 -dependence of
-dependence of 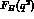 is again related to
the hadron structure, and mean squared-radii can be defined in
anology with eq.(10), i.e.,
is again related to
the hadron structure, and mean squared-radii can be defined in
anology with eq.(10), i.e.,
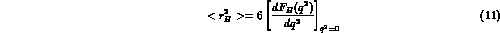
A simple example on the relation between these charge radii and the
quark substructure in hadrons is clearly offered by the low-mass
pseudoscalar mesons consisting of a spinless, s-wave 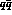 pair.
The squared charge radius of charged pions is
known to be about
pair.
The squared charge radius of charged pions is
known to be about 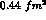 and can be attributed to the
distribution of the (positive) u and
and can be attributed to the
distribution of the (positive) u and 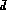 constituents of a
constituents of a  around their common CM.
In the
around their common CM.
In the 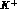 case, similarly,
the heavier
case, similarly,
the heavier  substitutes
substitutes 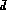 , thus reducing the
, thus reducing the 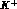 dimensions as corroborated by the data (see below).
Finally, the negatively charged
and light d-quark in a
dimensions as corroborated by the data (see below).
Finally, the negatively charged
and light d-quark in a 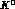 is worst localized than its
positively charged and heavier partner
is worst localized than its
positively charged and heavier partner  giving therefore rise
to the negative
giving therefore rise
to the negative 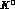 charge radius experimentally measured.
charge radius experimentally measured.