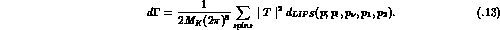
The partial decay rate for (5.1) is given by
The quantity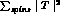 
is a Lorentz invariant quadratic
form in F,G,R and H. All scalar products can be expressed
in the 5 independent variables 
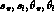and 
,
such that
Carrying out the integrations over the remaining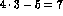 
variables
in (5.13) gives [51]
where
The form factors F,G,R and H are independent of 
and
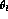. It is therefore possible to carry out two more
integrations in
(5.15) with the result
The explicit form of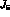 
is
For data analysis it is useful to represent this result in a still
different form which displays the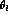 
and 
dependence more clearly [52]:
One obtains
where
The definition of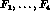 
in (5.21) corresponds
to the combinations used by Pais and Treiman [52] (the
different sign in the terms 
is due to our use of the metric
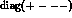). The form factors 
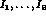agree with the expressions given in [52]. We conclude that our
convention for the relative phase in the definition of the form factors
in Eq. (5.12) agrees with the one used by Pais and Treiman.
The comparison of
(5.18) with
[53, table II,] shows furthermore that it also agrees with
this reference.
The quantity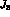 
can now easily be obtained from (5.19)
by integrating over 
and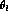 
,
