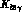 amplitudes were performed by Fearing, Fischbach and Smith
[50] using current algebra techniques.
amplitudes were performed by Fearing, Fischbach and Smith
[50] using current algebra techniques.
Prior to CHPT, the most detailed calculations of 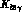 amplitudes were performed by Fearing, Fischbach and Smith
[50] using current algebra techniques.
amplitudes were performed by Fearing, Fischbach and Smith
[50] using current algebra techniques.
In the framework of CHPT, the amplitudes are given by (4.17) and (4.18) to leading order in the chiral expansion.
There are in general three types of contributions [44]:
anomaly, local contributions due to  and loop amplitudes.
and loop amplitudes.
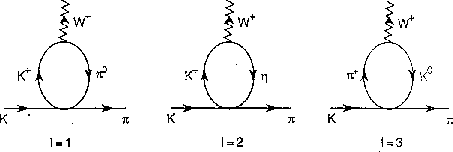
Figure 4.2: Loop diagrams (without tadpoles) for 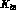 at
at 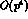 . For
. For
 , the photon must be appended on all charged lines and
on all vertices.
, the photon must be appended on all charged lines and
on all vertices.
The anomaly contributes to the axial amplitudes
The loop diagrams for 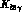 are shown in
Fig. 4.2. We first write the
are shown in
Fig. 4.2. We first write the 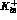 matrix element
in terms of three functions
matrix element
in terms of three functions 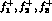 which will also appear
in the invariant amplitudes
which will also appear
in the invariant amplitudes 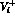 . Including the contributions
from the low-energy constants
. Including the contributions
from the low-energy constants 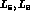 in
in 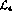 , the
, the
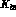 matrix element
matrix element 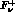 is given by
is given by
 is a scale independent coupling constant and we have traded
the tadpole contribution together with
is a scale independent coupling constant and we have traded
the tadpole contribution together with 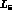 for
for 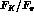 in
in
 . The sum over I corresponds to the three loop diagrams
of Fig. 4.2 with coefficients
. The sum over I corresponds to the three loop diagrams
of Fig. 4.2 with coefficients 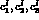 displayed in
table 4.3.
displayed in
table 4.3.

Table 4.3: Coefficients for the 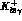 loop amplitudes
corresponding to the diagrams I=1,2,3 in Fig. 4.2.
All coefficients
loop amplitudes
corresponding to the diagrams I=1,2,3 in Fig. 4.2.
All coefficients 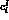 must be divided by
must be divided by
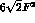 .
.
We use the Gell-Mann--Okubo mass formula
throughout to express 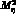 in terms of
in terms of  .
The functions
.
The functions  and
and 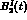 can be found in App. B.
can be found in App. B.
The standard 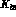 form factors
form factors 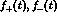 as given in the previous subsection [24] are
as given in the previous subsection [24] are
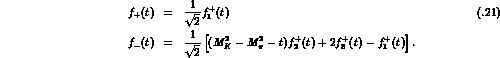
It remains to calculate the infrared finite tensor amplitude
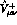 . The invariant amplitudes
. The invariant amplitudes 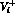 can be
expressed in terms of the previously defined functions
can be
expressed in terms of the previously defined functions 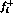 and of
additional amplitudes
and of
additional amplitudes 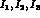 . Diagrammatically, the latter
amplitudes arise from those diagrams in Fig. 4.2 where the
photon is not appended on the incoming
. Diagrammatically, the latter
amplitudes arise from those diagrams in Fig. 4.2 where the
photon is not appended on the incoming 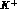 (non-Bremsstrahlung
diagrams). The final expressions are
(non-Bremsstrahlung
diagrams). The final expressions are
The amplitudes 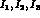 in Eq.(4.22) are given by
in Eq.(4.22) are given by
The function 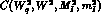 is given in App. B.
All the invariant amplitudes
is given in App. B.
All the invariant amplitudes 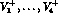 are
real in the physical region. Of course, the same is true for the
are
real in the physical region. Of course, the same is true for the
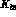 matrix element
matrix element 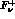 .
.
The 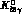 amplitude has a very similar structure. Both the
amplitude has a very similar structure. Both the
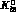 matrix element
matrix element 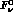 and the infrared finite
vector amplitude
and the infrared finite
vector amplitude 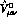 can be obtained from the
corresponding quantities
can be obtained from the
corresponding quantities 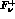 and
and
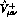 by the following steps:
by the following steps:
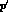 and
and 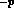 ;
;
 by
by 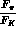 in
in 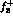 ;
;
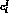 for
for
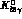 listed in table 4.4;
listed in table 4.4;
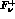 and
and 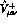 by a
factor
by a
factor 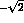 .
.

Table 4.4: Coefficients for the 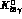 loop amplitudes
corresponding to the diagrams I=1,2,3 in Fig. 4.2. All
coefficients
loop amplitudes
corresponding to the diagrams I=1,2,3 in Fig. 4.2. All
coefficients 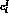 must be divided by
must be divided by 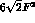 .
.
In calculating the rates with the complete amplitudes of the previous subsection, we use the same cuts as for the tree level rates in Subsect. 4.2:
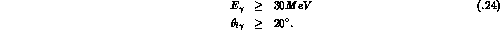
The physical values of 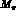 and
and 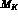 are used in the amplitudes.
are used in the amplitudes.
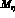 is calculated from the Gell-Mann--Okubo mass formula. The
values of the other parameters can be found in Ref. [2]
and in appendix A.
is calculated from the Gell-Mann--Okubo mass formula. The
values of the other parameters can be found in Ref. [2]
and in appendix A.
The results for 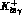 and
and 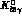 are displayed in
tables 4.5 and 4.6, respectively. For comparison, the
tree level branching ratios of table 4.1 and the rates for
the amplitudes without the loop contributions are also shown. The
separation between loop and counterterm contributions is of course
scale dependent. This scale dependence is absorbed in the scale invariant
constants
are displayed in
tables 4.5 and 4.6, respectively. For comparison, the
tree level branching ratios of table 4.1 and the rates for
the amplitudes without the loop contributions are also shown. The
separation between loop and counterterm contributions is of course
scale dependent. This scale dependence is absorbed in the scale invariant
constants 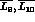 defined in Eqs.(4.20),
(4.23). In other words, the entries in tables 4.5,
4.6 for the amplitudes without loops correspond to setting
all coefficients
defined in Eqs.(4.20),
(4.23). In other words, the entries in tables 4.5,
4.6 for the amplitudes without loops correspond to setting
all coefficients 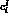 in tables 4.3,
4.4 equal to zero.
in tables 4.3,
4.4 equal to zero.
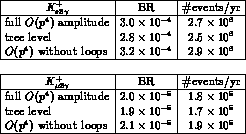
Table 4.5: Branching ratios and expected number of events at DA NE
for
NE
for 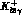 .
.

Table 4.6: Branching ratios and expected number of events at DA NE
for
NE
for 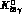 .
.