truecm
We know little about the real part of the Hamiltonian, the mass matrix M,
which is sensitive to virtual particle, high-energy effects (this is,
for instance, the case in the Standard Theory, where T violation in M is
determined by top-quark exchange). On the other hand, unitarity relates
the matrix 
, the imaginary part of H, to the real decays of
the neutral Kaons, about which we have considerably more information:
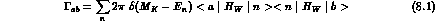
In particular, we know that the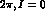 
final state is by far the most
prominent one in 
and 
decays, and this simple fact gives
interesting restrictions on the parameters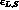 
.
We start from Eqs. (1.16) to (1.18), which are easily solved to obtain h-n, l and m in terms of the physical parameters. Separating real and imaginary parts, one finds six relations:
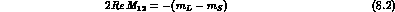
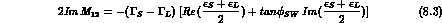
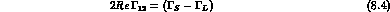
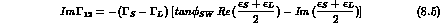
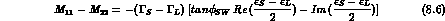
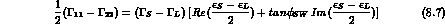
We have introduced the "superweak phase",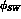 
, defined by:
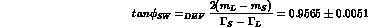
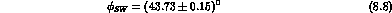
and will denote by v and w the complex numbers:
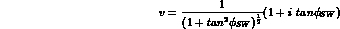
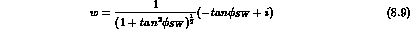
Eqs. (8.3) and (8.5) specify the components of
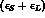along v and w, regarded as mutually orthogonal
vectors in the complex plane. Eqs. (8.6) and (8.7) do the same for the CPT
violating parameter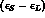 
.
In the first case, we use the fact that the dominant 2
, I=0 amplitude is
exactly real, in the Wu-Yang convention. Correspondingly,
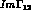receives contribution from 2
with I=2, 3
and semileptonic decay
modes. In general, the scale of these contributions is suppressed, with respect
to the r.h.s. of Eq.(8.5), by a factor of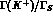 
or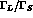 
. Thus, to be competitive with the r.h.s., CP violation
on the l.h.s. of Eq. (8.5) should be of order unity, which is not the case
(rather, as we have indicated in Sect. 5, 
effects in
2
decays are much more suppressed).
More in detail, one may classify the contribution of the most prominent intermediate states as follows (first order terms only are retained).
2
:
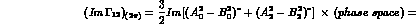
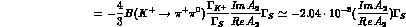
3
:
We approximate 3
decay amplitudes with their value at the center of the
Dalitz plot and consider only the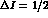 
contribution to the
CP-conserving transition. Defining CP-violating parameters according
to [4]:
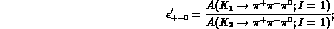
one finds:
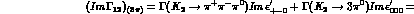
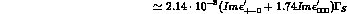
semileptonic:
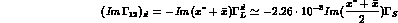
(we have averaged the electron and muon contributions). The
semileptonic contribution is suppressed, since it requires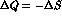 
.
Neglecting completely the l.h.s of (8.5), we conclude
that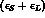 
is orthogonal to w:
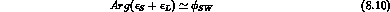
The component along v is determined by the short-distance sensitive
quantity,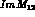 
:
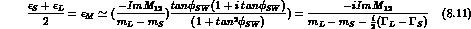
In addition, since:
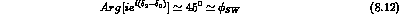
it follows from Eq. (4.12) that 
is approximately
parallel to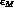 
, except for CPT-violating effects.
To make a similar analysis for the CPT-violating quantity,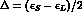 
, we first extract the 2
contribution to the
r.h.s. of Eq. (8.7). Explicitly (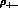
, 
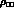are the 2
phase-space factors; 
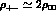for exact isospin symmetry):
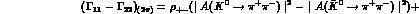
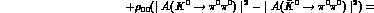
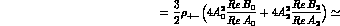
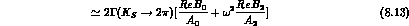
With this result, Eq. (8.7) becomes:
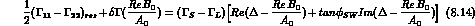
The suffix res indicates the sum over intermediate states
different from 2
, I=0, and:
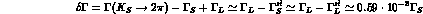
(assuming the semileptonic rates af K
and K
to be
approximately equal).
The term proportional to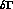 
can be safely
neglected.
Proceeding as
before, we write the most important contributions to the l.h.s. of Eq. (8.14)
as follows.
2
, I=2:
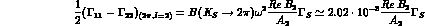
3
:
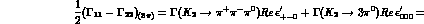
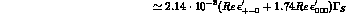
semileptonic:
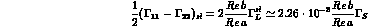
(electron and muon contributions averaged).
It is difficult to say anything more precise about the first term in the
l.h.s. of (8.14), except that it should be very small, for the same reasons
which justified the neglect of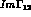 
.
DA
NE can improve
substantially on the present limits to the above CPT-violating quantities and
therefore lead to improved bounds to the unitarity sum.
If we take the l.h.s. to vanish, Eq. (8.14) leads to the elegant result
that the complex number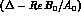 
is parallel
to w, i.e. it is orthogonal to 
:
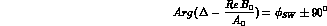
so that:
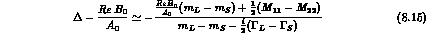
or, equivalently:
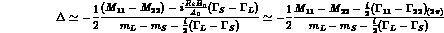
The situation is illustrated in Fig. 2 (without paying attention to the relative proportions).
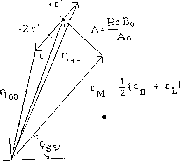
Figure 2: Schematic representation in the complex plane, of the relations
between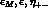 
and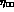 
. 
is
drawn approximately parallel to 
, as appropriate in the
exact CPT limit. Relative sizes are not in scale.
The phases of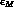 
and 
are sometime discussed, in the
literature, in connection with the Bell-Steinberger (BS) relation [23]:
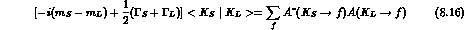
The BS relation can be derived directly from the conservation of probability.
By substituting Eqs. (1.12) and (1.13) in the r.h.s. of (8.16), it is immediate to see that the real and imaginary parts of the BS relation coincide with Eqs. (8.7) and (8.5), respectively.
It could have not been differently. The unitarity condition Eq.(8.1) is all
we can say about probability conservation. The BS equation involves a total of
4 real quantities: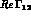 
,
, 
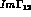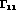and 
. 
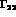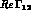and the average
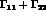are related to the CP and CPT conserving total
widths,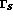 
and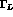 
; the CP-violating (CPT-conserving)
determines the phase
of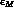 
, while the CPT and CP violating difference,
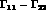, fixes the phase of the combination 
.
There can be no other general restrictions.