


Next: 10 The impact of
Up: Chpter 1 Section 1
Previous: 8 Unitarity constraints
truecm
We can analyse the data at different levels, according to whether CPT
symmetry and the 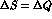 rule are kept exact or released in the
semileptonic transitions. Exact CPT and the
rule are kept exact or released in the
semileptonic transitions. Exact CPT and the 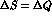 rule are
assumed by Barmin et al. [6], who adopt what we have called
Scheme I, while Buchanan et al. [1] adopt Scheme II. We
illustrate in detail, in this Section, the results in the Scheme I,
and will comment, in the next Section, on the impact of DA
rule are
assumed by Barmin et al. [6], who adopt what we have called
Scheme I, while Buchanan et al. [1] adopt Scheme II. We
illustrate in detail, in this Section, the results in the Scheme I,
and will comment, in the next Section, on the impact of DA NE on the
complex of Kaon parameters in Schemes II and III.
truecm
NE on the
complex of Kaon parameters in Schemes II and III.
truecm
Data [13]:
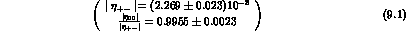
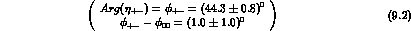
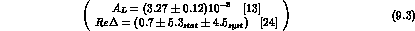
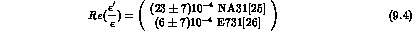
truecm
Analysis:
The smallness of  implies that
implies that  is very close to
is very close to
 and
and 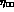 :
:
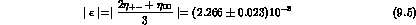
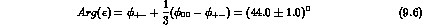
With the most recent analysis of the data there is no indication of a possible
CPT-violating difference between  and
and 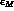 .
With
.
With 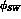 the superweak phase, Eq. (8.8), we have:
the superweak phase, Eq. (8.8), we have:
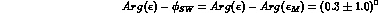
Since  is at right angle with
respect to
is at right angle with
respect to 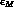 , see Fig. 2, the above result translates into:
, see Fig. 2, the above result translates into:
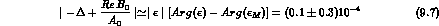
In Scheme I, the K lepton asymmetry, Eq. (9.3), already allows a
separate determination of
lepton asymmetry, Eq. (9.3), already allows a
separate determination of  and
and 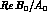 .
From (9.3) we get:
.
From (9.3) we get:
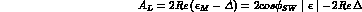
whence:

Since, as we saw:
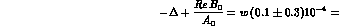
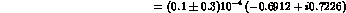
we find at once:
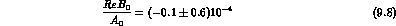
and:
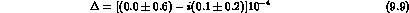
Note that this result is still more precise than the direct measurement of
CP-LEAR [24] quoted in (9.3).
Using Eq. (8.6), we find a limit to the CPT-violating
mass difference, M
M -M
-M :
:
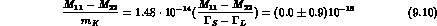
A last possible CPT test is given by the phase of
 /
/ . As seen from Eq. (4.12), the phase of
. As seen from Eq. (4.12), the phase of
 /
/ is made of two components:
is made of two components:

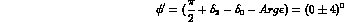
A precise measurement of the real and imaginary parts of
 /
/ allows, in principle, a determination of the CPT
violating phase,
allows, in principle, a determination of the CPT
violating phase,  . The
smallness of
. The
smallness of  , Eq. (9.4), implies
, Eq. (9.4), implies
 , so that we can obtain anyway
an interesting bound to the CPT violating part of
, so that we can obtain anyway
an interesting bound to the CPT violating part of  /
/ .
In formulae, from Eqs. (4.9), (4.10) and (4.12), one finds:
.
In formulae, from Eqs. (4.9), (4.10) and (4.12), one finds:

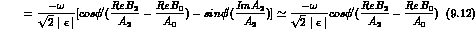
so that:
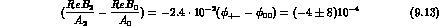
Note that the error of the strong interaction phase drops out in
first order, because 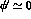 .
.
It will be difficult to make this into a much more precise test.
DA NE can produce, anyway, a substantial improvement on the determination
of Im(
NE can produce, anyway, a substantial improvement on the determination
of Im( /
/ ) and of the strong interaction phase.
) and of the strong interaction phase.



Next: 10 The impact of
Up: Chpter 1 Section 1
Previous: 8 Unitarity constraints
Carlos E.Piedrafita
 rule are kept exact or released in the
semileptonic transitions. Exact CPT and the
rule are kept exact or released in the
semileptonic transitions. Exact CPT and the 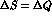 rule are
assumed by Barmin et al. [6], who adopt what we have called
Scheme I, while Buchanan et al. [1] adopt Scheme II. We
illustrate in detail, in this Section, the results in the Scheme I,
and will comment, in the next Section, on the impact of DA
rule are
assumed by Barmin et al. [6], who adopt what we have called
Scheme I, while Buchanan et al. [1] adopt Scheme II. We
illustrate in detail, in this Section, the results in the Scheme I,
and will comment, in the next Section, on the impact of DA NE on the
complex of Kaon parameters in Schemes II and III.
truecm
NE on the
complex of Kaon parameters in Schemes II and III.
truecm
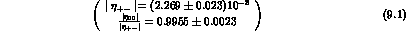
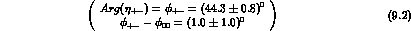
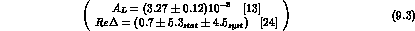
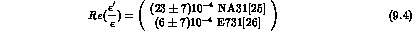
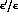 implies that
implies that  is very close to
is very close to
 and
and  :
:
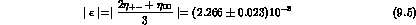
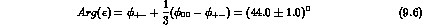
 and
and  .
With
.
With  the superweak phase, Eq. (8.8), we have:
the superweak phase, Eq. (8.8), we have:
 is at right angle with
respect to
is at right angle with
respect to  , see Fig. 2, the above result translates into:
, see Fig. 2, the above result translates into:
 lepton asymmetry, Eq. (9.3), already allows a
separate determination of
lepton asymmetry, Eq. (9.3), already allows a
separate determination of  and
and  .
From (9.3) we get:
.
From (9.3) we get:

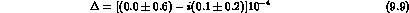
 -M
-M :
:
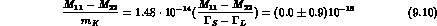
 /
/ . As seen from Eq. (4.12), the phase of
. As seen from Eq. (4.12), the phase of
 /
/ is made of two components:
is made of two components:

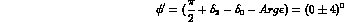
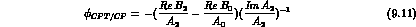
 /
/ allows, in principle, a determination of the CPT
violating phase,
allows, in principle, a determination of the CPT
violating phase, 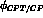 . The
smallness of
. The
smallness of 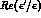 , Eq. (9.4), implies
, Eq. (9.4), implies
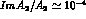 , so that we can obtain anyway
an interesting bound to the CPT violating part of
, so that we can obtain anyway
an interesting bound to the CPT violating part of  /
/ .
In formulae, from Eqs. (4.9), (4.10) and (4.12), one finds:
.
In formulae, from Eqs. (4.9), (4.10) and (4.12), one finds:

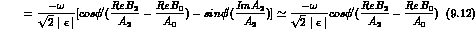
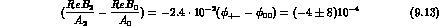
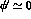 .
. NE can produce, anyway, a substantial improvement on the determination
of Im(
NE can produce, anyway, a substantial improvement on the determination
of Im( /
/ ) and of the strong interaction phase.
) and of the strong interaction phase.