


Next: 3 The Zweig rule
Up: 2 Probing the nature
Previous: 2.1 Calculation of the
Suppose that 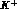 and
and 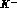 with three momenta
with three momenta 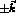 produce an extended
scalar meson in its rest frame. The interaction Hamiltonian
produce an extended
scalar meson in its rest frame. The interaction Hamiltonian 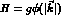 is in
general a function of momentum. Now make the replacement
is in
general a function of momentum. Now make the replacement 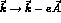 , expand
, expand 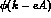 to leading order in e and one
finds a new electromagnetic contribution
to leading order in e and one
finds a new electromagnetic contribution
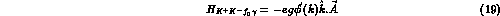
The effect of this form factor is readily seen in time ordered perturbation theory. There are
four contributions: (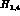 are figs 2a, c, while
are figs 2a, c, while 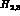 are fig b where the
are fig b where the 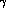 is emitted from the
is emitted from the 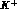 or
or 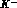 leg). We write these (for momentum routing see fig 3)
leg). We write these (for momentum routing see fig 3)
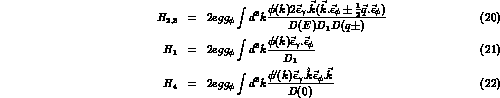
where
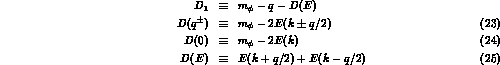
where 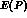 is the energy of a kaon with momentum P.
Note that
is the energy of a kaon with momentum P.
Note that 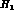 is the (form factor modified) contact diagram and
is the (form factor modified) contact diagram and 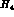 is the new
contribution arising from the extended
is the new
contribution arising from the extended 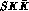 vertex.
vertex.
After some manipulations their sum can be written
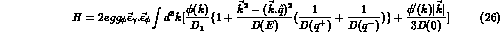
If 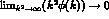 we may integrate the final
term in eq (2.18) by parts and obtain for it
we may integrate the final
term in eq (2.18) by parts and obtain for it
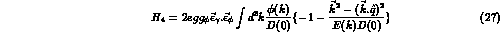
This is identical to the 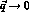 limit of
limit of 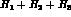 , and hence we
see explicitly that the
, and hence we
see explicitly that the 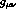 term (i.e. the
term (i.e. the
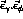 as calculated above) is effectively subtracted
at
q=0 due to the partial integration of the
as calculated above) is effectively subtracted
at
q=0 due to the partial integration of the 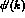 contribution,
contribution, 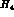 .
.
If one now has a model for 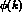 one can perform the integrals in eq (2.18)
numerically.
one can perform the integrals in eq (2.18)
numerically.
For the KK molecule the wavefunction

is a solution of the Schrodinger equation
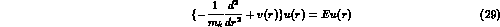
where (ref 13) one approximates
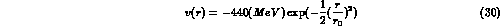
with 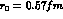 and hence E=- 10 MeV. This equation may be solved numerically
and, for analytic purposes, we find that the
and hence E=- 10 MeV. This equation may be solved numerically
and, for analytic purposes, we find that the 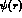 is well approximated by
is well approximated by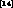 (fig 4)
(fig 4)
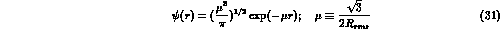
where  (thus
(thus 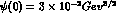 , see also ref
13). The momentum space wave function that is used in our computation is thus
, see also ref
13). The momentum space wave function that is used in our computation is thus
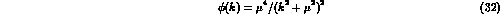
The rate for 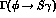 is shown as a function of
is shown as a function of
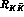 in fig (5). The non relativistic approximation eqs (2.12-2.19) is valid for
in fig (5). The non relativistic approximation eqs (2.12-2.19) is valid for
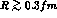 which is applicable to the KK molecule: for
which is applicable to the KK molecule: for 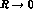 the
fully relativistic formalism is required and has been included in the curve displayed in fig
5. As
the
fully relativistic formalism is required and has been included in the curve displayed in fig
5. As 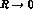 and
and 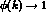 we recover the
numerical result of the pointlike field theory whereas for the specific
we recover the
numerical result of the pointlike field theory whereas for the specific 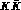 molecule
wavefunction above one predicts a branching ratio of some
molecule
wavefunction above one predicts a branching ratio of some 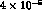 (width
(width
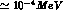 ). This is only
). This is only
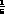 of the pointlike field theory result but is larger than that expected for the
production rate of a
of the pointlike field theory result but is larger than that expected for the
production rate of a
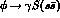 scalar meson.
scalar meson.
Note that at 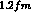 the system is in some sense a mixture between genuinely separate
the system is in some sense a mixture between genuinely separate
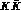 (which require
(which require 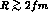 ) and a compact
) and a compact 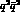 system.
These results and their interpretation are still preliminary. Some of the questions that
they bear on are discussed in the next section.
system.
These results and their interpretation are still preliminary. Some of the questions that
they bear on are discussed in the next section.



Next: 3 The Zweig rule
Up: 2 Probing the nature
Previous: 2.1 Calculation of the
Carlos E.Piedrafita
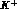 and
and 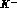 with three momenta
with three momenta 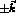 produce an extended
scalar meson in its rest frame. The interaction Hamiltonian
produce an extended
scalar meson in its rest frame. The interaction Hamiltonian 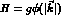 is in
general a function of momentum. Now make the replacement
is in
general a function of momentum. Now make the replacement 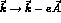 , expand
, expand 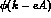 to leading order in e and one
finds a new electromagnetic contribution
to leading order in e and one
finds a new electromagnetic contribution
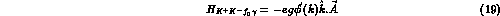
 are figs 2a, c, while
are figs 2a, c, while  are fig b where the
are fig b where the 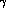 is emitted from the
is emitted from the 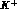 or
or 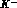 leg). We write these (for momentum routing see fig 3)
leg). We write these (for momentum routing see fig 3)
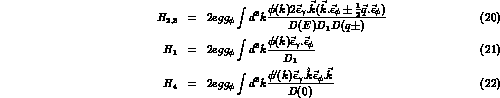
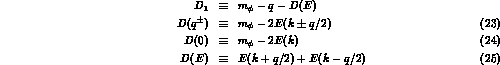
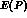 is the energy of a kaon with momentum P.
Note that
is the energy of a kaon with momentum P.
Note that 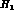 is the (form factor modified) contact diagram and
is the (form factor modified) contact diagram and 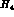 is the new
contribution arising from the extended
is the new
contribution arising from the extended  vertex.
vertex.
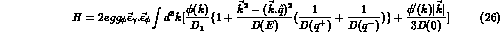
 we may integrate the final
term in eq (2.18) by parts and obtain for it
we may integrate the final
term in eq (2.18) by parts and obtain for it
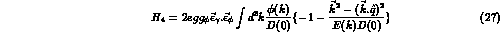
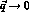 limit of
limit of 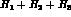 , and hence we
see explicitly that the
, and hence we
see explicitly that the 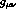 term (i.e. the
term (i.e. the
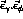 as calculated above) is effectively subtracted
at
q=0 due to the partial integration of the
as calculated above) is effectively subtracted
at
q=0 due to the partial integration of the 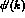 contribution,
contribution, 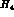 .
.
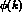 one can perform the integrals in eq (2.18)
numerically.
one can perform the integrals in eq (2.18)
numerically.

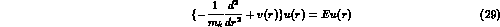
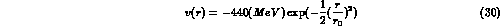
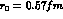 and hence E=- 10 MeV. This equation may be solved numerically
and, for analytic purposes, we find that the
and hence E=- 10 MeV. This equation may be solved numerically
and, for analytic purposes, we find that the 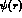 is well approximated by
is well approximated by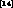 (fig 4)
(fig 4)
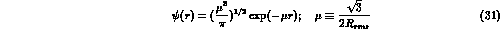
 (thus
(thus 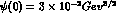 , see also ref
13). The momentum space wave function that is used in our computation is thus
, see also ref
13). The momentum space wave function that is used in our computation is thus
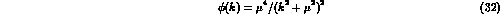
 is shown as a function of
is shown as a function of
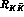 in fig (5). The non relativistic approximation eqs (2.12-2.19) is valid for
in fig (5). The non relativistic approximation eqs (2.12-2.19) is valid for
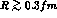 which is applicable to the KK molecule: for
which is applicable to the KK molecule: for 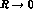 the
fully relativistic formalism is required and has been included in the curve displayed in fig
5. As
the
fully relativistic formalism is required and has been included in the curve displayed in fig
5. As 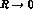 and
and 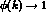 we recover the
numerical result of the pointlike field theory whereas for the specific
we recover the
numerical result of the pointlike field theory whereas for the specific 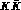 molecule
wavefunction above one predicts a branching ratio of some
molecule
wavefunction above one predicts a branching ratio of some 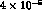 (width
(width
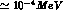 ). This is only
). This is only
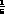 of the pointlike field theory result but is larger than that expected for the
production rate of a
of the pointlike field theory result but is larger than that expected for the
production rate of a
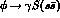 scalar meson.
scalar meson.
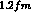 the system is in some sense a mixture between genuinely separate
the system is in some sense a mixture between genuinely separate
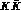 (which require
(which require 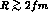 ) and a compact
) and a compact 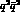 system.
These results and their interpretation are still preliminary. Some of the questions that
they bear on are discussed in the next section.
system.
These results and their interpretation are still preliminary. Some of the questions that
they bear on are discussed in the next section.