 and K interactions gauge invariant, one finds for charged
kaons
and K interactions gauge invariant, one finds for charged
kaons
Upon making the  and K interactions gauge invariant, one finds for charged
kaons
and K interactions gauge invariant, one finds for charged
kaons
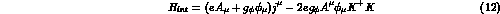
where 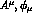 and K are the photon, phi and charged kaon fields,
and K are the photon, phi and charged kaon fields,
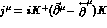 . Upon
recombining the two kaons to form a pointlike scalar field, gauge invariance
generates no extra diagram and the resulting diagrams are in figs (1). Immediately one
notes a problem: the contact diagram fig 1a diverges. The trick has been to calculate the
finite fig (1b) and then, by appealing to gauge invariance, to abstract a finite answer. This
is done either by
. Upon
recombining the two kaons to form a pointlike scalar field, gauge invariance
generates no extra diagram and the resulting diagrams are in figs (1). Immediately one
notes a problem: the contact diagram fig 1a diverges. The trick has been to calculate the
finite fig (1b) and then, by appealing to gauge invariance, to abstract a finite answer. This
is done either by
a) [Refs 1-3], Fig 1a contributes, to 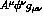 whereas Fig 1b
contributes both to this and to
whereas Fig 1b
contributes both to this and to 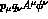 . Therefore one
need calculate only fig 1b, abstract the finite coefficient of the
. Therefore one
need calculate only fig 1b, abstract the finite coefficient of the 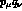 term and,
by gauge invariance, one is assured that this must be the finite result.
term and,
by gauge invariance, one is assured that this must be the finite result.
b) [Ref 5] Compute the imaginary part of the amplitude (which arises only from fig 1b) and write a subtracted dispersion relation, with the subtraction constrained by gauge invariance.
We have considered the case where the scalar meson is an extended object, in
particular a
have considered the case where the scalar meson is an extended object, in
particular a 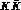 bound state. The
bound state. The 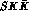 vertex therefore involves a
momentum dependent form factor
vertex therefore involves a
momentum dependent form factor 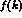 , where k is the kaon, or loop, momentum
which will be scaled in
, where k is the kaon, or loop, momentum
which will be scaled in 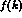 by
by 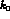 , the mean momentum in the bound state
wavefunction or, in effect, the inverse size of the system. In the limit where
, the mean momentum in the bound state
wavefunction or, in effect, the inverse size of the system. In the limit where
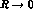 (or
(or 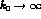 ) we recover the formal results of approaches
) we recover the formal results of approaches
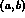 above, as we must, but our approach offers some possible new insights into the
physical
processes at work. In particular there is a further diagram (fig 2c) proportional to
above, as we must, but our approach offers some possible new insights into the
physical
processes at work. In particular there is a further diagram (fig 2c) proportional to
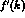 since the minimal substitution yields
since the minimal substitution yields
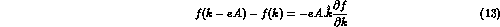
As we shall see, this exactly cancels the contribution from the seagull diagram fig 2a in the
limit where 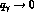 , and
gives an expression for the finite amplitude which is explicitly in the form of a difference
, and
gives an expression for the finite amplitude which is explicitly in the form of a difference
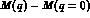 ; this makes contact with the subtracted dispersion relation approach of ref. 5.
; this makes contact with the subtracted dispersion relation approach of ref. 5.
First let us briefly summarise the Feynman diagram in the standard pointlike field theory
as it has caused some problems in refs (2,3). If we denote  then the tensor for fig (3 ) may be written (compare
refs 2,3 eqs 8 & 6)
then the tensor for fig (3 ) may be written (compare
refs 2,3 eqs 8 & 6)
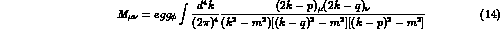
We will read off the coefficient of 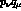 after combining the denominators by the
standard Feynman trick so that
after combining the denominators by the
standard Feynman trick so that
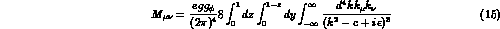
where 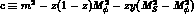 , and the
, and the 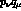 term appears when we make the shift
term appears when we make the shift
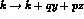 .
One obtains
.
One obtains
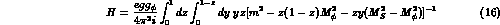
Note that 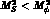 and so one has to take care when performing the
and so one has to take care when performing the 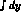 . One obtains (recall
. One obtains (recall 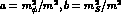 )
)
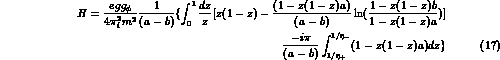
where
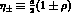 with
with 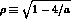 .
.
I have exhibited these manipulations in order to assess the existing literature. In ref (2),
the (unnumbered) eq 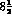 has omitted the imaginary part - the final integral
above. In ref (3) at eq 7 one can see how this has arisen: the coefficient of their term
has omitted the imaginary part - the final integral
above. In ref (3) at eq 7 one can see how this has arisen: the coefficient of their term
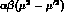 corresponds to
corresponds to 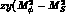 ) in our
eq (2.8) i.e. it has the opposite sign. However, as ref (3) then proceeds to neglect this term
one might think that the discrepancy would not matter - but there is no need to ignore this
term as the integrals can be performed analytically and one sees that the said term is not
negligible.
) in our
eq (2.8) i.e. it has the opposite sign. However, as ref (3) then proceeds to neglect this term
one might think that the discrepancy would not matter - but there is no need to ignore this
term as the integrals can be performed analytically and one sees that the said term is not
negligible.
In performing the integrals, take care to note that a>4 whereas b<4 (which causes
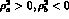 ). Hence one confirms the
). Hence one confirms the  as given in ref (1) [our
calculation above has referred only to the diagram where the
as given in ref (1) [our
calculation above has referred only to the diagram where the 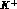 emits the
emits the 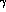 ;
the contribution for the
;
the contribution for the 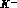 gives the same and so the total amplitude is double that of
eq (2.9), hence in quantitative agreement with eqs (3 and 4) of ref (1)]. Straightforward
algebra confirms that this equals the eqs (9-11) of ref (5).
gives the same and so the total amplitude is double that of
eq (2.9), hence in quantitative agreement with eqs (3 and 4) of ref (1)]. Straightforward
algebra confirms that this equals the eqs (9-11) of ref (5).
Numerical evaluation, using  ,
, 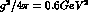 leads to
leads to
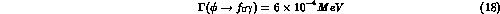
in contrast to the value of 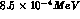 (J Pestieau, private communication,
confirms our value at eq 2.10). In ref (5) the rate for
(J Pestieau, private communication,
confirms our value at eq 2.10). In ref (5) the rate for 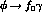 is not
directly quoted, though as their expression agrees with ours, one supposes that the value at
eq (2.10) should obtain. Instead, ref (5) gives values for
is not
directly quoted, though as their expression agrees with ours, one supposes that the value at
eq (2.10) should obtain. Instead, ref (5) gives values for 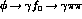 (for example) and claims that this depends upon
the
(for example) and claims that this depends upon
the 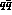 or
or
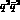 structure of the
structure of the 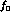 . However, the differences in rate (which vary by an
order of magnitude between
. However, the differences in rate (which vary by an
order of magnitude between 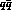 and
and 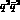 models) arise because different
magnitudes for the fKK couplings have entered. In the
models) arise because different
magnitudes for the fKK couplings have entered. In the
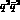 model a value for
model a value for 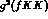 was used identical to ours and, if one
assumes
100% branching ratio for
was used identical to ours and, if one
assumes
100% branching ratio for  , the rate is consistent with our eq (2.10)
[ref 5 has integrated over the resonance]: Ref 5 notes that in the
, the rate is consistent with our eq (2.10)
[ref 5 has integrated over the resonance]: Ref 5 notes that in the  model the
relation between
model the
relation between 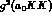 and
and  imply
imply 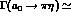 275 MeV. In the
275 MeV. In the 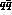 model ref 5 uses as
input
the experimental value of
model ref 5 uses as
input
the experimental value of  55 MeV which
implies a reduced value for
55 MeV which
implies a reduced value for 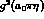 and, therefore, for
and, therefore, for 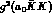 : the
predicted
rate for
: the
predicted
rate for 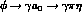 is correspondingly
reduced.
is correspondingly
reduced.
Thus we believe that the apparent discrimination among models in ref 5 is rather indirect
and logically suspect in the case of 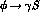 . The calculation has
assumed a pointlike scalar field which couples to pointlike kaons with a strength that can
be extracted from experiment. The computation of a rate for
. The calculation has
assumed a pointlike scalar field which couples to pointlike kaons with a strength that can
be extracted from experiment. The computation of a rate for  will depend upon this strength and cannot of itself
discriminate among models of internal structure for the S.
will depend upon this strength and cannot of itself
discriminate among models of internal structure for the S.
We have considered the production of an extended scalar meson which is treated as
a KK system (following the work of ref 8). Our results numerically agree with the
pointlike field theory as
have considered the production of an extended scalar meson which is treated as
a KK system (following the work of ref 8). Our results numerically agree with the
pointlike field theory as 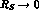 , and the branching ratio falls for
, and the branching ratio falls for 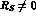 . A genuine KK molecule will have
. A genuine KK molecule will have 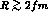 in order that two colour
singlet
in order that two colour
singlet 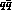 states are meaningful - the resulting width
states are meaningful - the resulting width  .
At the other extreme, where the
.
At the other extreme, where the 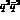 are all contained within a single 1 fm
confinement domain one recovers the result of eq (2.10) and ref 5. Thus we suspect that
that
large branching ratio corresponds to a P-matrix state (ref 9).
are all contained within a single 1 fm
confinement domain one recovers the result of eq (2.10) and ref 5. Thus we suspect that
that
large branching ratio corresponds to a P-matrix state (ref 9).