Massimo Pietroni

Sezione INFN di Padova

Ottant’anni fa Theodor Kaluza ipotizzò l’esistenza di nuove dimensioni spaziali, oltre alle tre della nostra percezione. Secondo l’ipotesi originaria, queste sarebbero invisibili perché “arrotolate” su se stesse, con raggi dell’ordine della lunghezza di Planck (10-32 m). In questi ultimi anni lo scenario è cambiato in modo radical e si pofila la possibilità che le nuove dimensioni abbiano raggi poco più piccoli di un millimetro e la loro presenza, legata alla gravità quantistica, venga scoperta all’acceleratore LHC in costruzione al CERN.

Negli anni venti del secolo scorso, il matematico polacco Theodor Kaluza ­ripreso in seguito dallo svedese Oskar Klein­ fece un’osservazione sorprendente. Si chiese che aspetto avrebbe la teoria della gravitazione di Einstein se lo spazio anziché tre dimensioni ne avesse quattro. La risposta ­almeno a prima vista­ sembrava la realizzazione del sogno einsteniano della teoria unificata: in questo spazio più grande il gravitone (la particella che media la forza di gravità) ed il fotone (il mediatore dell’interazione elettromagnetica) sarebbero parenti strettissimi. In altre parole la gravitazione di Einstein e l’elettromagnetismo di Maxwell, che dal nostro punto di vista di osservatori tridimensionali sono così diversi, sarebbero manifestazioni di una stessa teoria: la gravitazione del mondo a quattro dimensioni di Kaluza e Klein.

La proposta di Kaluza e Klein, nella sua forma originaria, non resse ad un esame più approfondito. Tuttavia, l’idea che l’unificazione tra le interazioni fondamentali potesse essere realizzata considerando uno spazio con più di tre dimensioni continuò a fluire in modo carsico nel sottosuolo della fisica teorica, per riemergere infine con autorevolezza negli anni ottanta nell’ambito delle teorie di superstringa, che addirittura prevedono sei (o sette) dimensioni in più (Fig.1).

Perché non le vediamo?

È evidente che la prima domanda che sorge non appena si comincia a ragionare su un’ipotesi a prima vista tanto bizzarra è come sia possibile che queste dimensioni “extra” non vengano percepite dai nostri sensi e nemmeno dagli apparati sperimentali più accurati di cui disponiamo.

Sostanzialmente, possiamo immaginare due tipi di risposte. La prima, quella data già da Kaluza e Klein, è che le nuove dimensioni sono “piccolissime”. In questo scenario, mentre le tre dimensioni ordinarie si estendono per una distanza infinita (o almeno dell’ordine delle dimensioni dell’universo), le dimensioni extra sono invece limitate, formando dei piccoli segmenti o dei cerchietti. Viaggiando lungo una di queste dimensioni, dopo un breve percorso ci si ritrova al punto di partenza, o ci si scontra con una barriera invalicabile (Fig.2). Più piccole sono queste dimensioni, maggiore è l’energia necessaria per vederle. Se la loro estensione è pari a R, bisogna raggiungere una risoluzione spaziale inferiore di R, ma questo, per il principio di Heisenberg valido nel microcosmo, richiede impulsi tipici superiori a 1/R (in opportune unità di misura). Ci vuole insomma molta energia per entrare nelle dimensioni compatte, e se R è sufficientemente piccolo, ad esempio 10-19 m, l’energia necessaria è pari ad 1000 GeV, e quindi superiore a quella disponibile negli odierni acceleratori.

L’altro modo per spiegare “l’invisibilità” delle dimensioni extra è immaginare che queste siano inaccessibili alle particelle che usiamo come sonde sperimentali. In questo scenario la situazione è analoga a quella in cui si trova una formica cieca che si muove sul piano di un tavolo: completamente inconsapevole della terza dimensione che si alza sopra la sua testa, questa è convinta di vivere in un mondo bidimensionale. Situazione ben differente rispetto a quella del moscerino che, oltre a camminare sul tavolo, può librarsi in aria. Analogamente, se per sondare lo spazio-tempo usiamo delle particelle (fotoni, elettroni, protoni...) che non hanno accesso a eventuali ulteriori dimensioni, non c’è nessun modo in cui queste possano essere messe in evidenza. Se è così, queste dimensioni inaccessibili possono essere anche molto grandi, perfino infinite.

Dimensioni extra nelle teorie attuali

Una delle scoperte più interessanti della fisica teorica di questi ultimi anni, e in particolare della teoria delle stringhe, consiste proprio nell’aver fornito una base consistente a questo scenario, che a prima vista potrebbe sembrare campato in aria. Secondo la teoria delle stringhe è possibile, per esempio, che i gravitoni si muovano in tutte le nove o dieci dimensioni spaziali, grandi e piccole (analogamente ai moscerini), e che le particelle del modello standard siano confinate in uno spazio con meno dimensioni (le formiche cieche). È chiaro allora che in questo caso gli esperimenti che utilizzano leptoni, adroni o fotoni, potranno dare informazioni solo sulle dimensioni in cui viaggiano queste particelle, mentre le dimensioni in cui viaggiano solo i gravitoni potranno essere analizzate solamente con esperimenti di tipo gravitazionale.

Mentre per le dimensioni extra in cui vivono anche le particelle del modello standard resta valido il discorso fatto per lo scenario alla Kaluza-Klein ­se avessero raggi superiori a 10-18 m avrebbero dovuto venir osservate agli acceleratori attuali­ le dimensioni puramente “gravitazionali”, quelle cioè in cui viaggiano solo i gravitoni, potrebbero essere molto più grandi, arrivando adirittura a valori di poco inferiori al millimetro!

Il modo migliore per metterle in evidenza è quello di studiare la forza di gravità fra due masse separate da una piccola distanza. Infatti, se a una distanza R si aprissero n nuove dimensioni per i gravitoni, la legge di Newton fra due masse m1 e m2 poste a distanza r

F=GN m1 m²/r²

verrebbe modificata per separazioni r molto più piccole di R, assumendo la forma (3+n)-dimensionale

F=G m1 m²/r²+n

che non è più inversamente proporzionale al quadrato di r e dove, inoltre, compare una nuova costante, G, al posto della costante di Newton, GN. La relazione tra le due costanti si ottiene osservando che le due espressioni devono dare luogo alla stessa forza quando la separazione è al valore di confine r=R, il che richiede

G=Rn GN .

Per quello che se ne sa dal punto di vista sperimentale, a distanze inferiori al millimetro la forza di gravità fra due masse potrebbe avere un comportamento completamente diverso da quello previsto dalla legge di Newton. Per questo motivo, lo scenario che abbiamo appena delineato ha dato il via ad una serie di progetti per la ricerca di eventuali deviazioni dalla legge dell’inverso del quadrato della distanza (e a progetti analoghi per la misura dell’effetto Casimir). Attualmente, i limiti migliori sono quelli ottenuti dall’esperimento Eötwash, dell’università di Washington, che consentono di escludere dimensioni extra di raggio R superiore ai 200 micron.

Perché la gravità è così debole rispetto alle altre interazioni?

Un secondo aspetto interessante di questo scenario è invece di natura più squisitamente teorica ed ha a che vedere con il cosiddetto “problema della gerarchia”, ossia della spiegazione della debolezza estrema della gravità in confronto alle altre interazioni (basti pensare che la forza di gravità fra due protoni è più piccola di quella elettrostatica per un fattore circa 1037). Nell’ottica extra-dimensionale la spiegazione di questo fatto è prettamente geometrica. A distanze estremamente piccole, dell’ordine di 10-19 m, la gravità sarebbe forte come le altre interazioni, e quindi non ci sarebbe, a livello fondamentale, nessun problema di gerarchia. Per distanze più grandi, ma più piccole del millimetro, le altre interazioni sarebbero già “tridimensionali“, mentre la gravità continuerebbe a diffondersi non solo nelle tre dimensioni spaziali ma anche nelle dimensioni in più, e quindi la sua forza decrescerebbe più rapidamente con la distanza, secondo la legge 1/r²⁺ⁿ. Infine, a distanze maggiori del millimetro, anche la gravità diventerebbe tridimensionale e quindi comincerebbe a seguire la legge 1/r², ma nel frattempo si sarebbe estremamente indebolita rispetto alle altre interazioni.

Come è immaginabile, uno scenario così radicale è stato setacciato in lungo e in largo allo scopo di mettere in evidenza possibili inconsistenze con i risultati sperimentali. Sorprendentemente, fino ad ora tutti i test sono stati superati. L’aspetto più peculiare è senza dubbio rappresentato dal fatto che, come abbiamo visto, gli effetti gravitazionali, solitamente trascurabili rispetto a quelli delle interazioni forti ed elettrodeboli, possono essere qui dello stesso ordine di grandezza, e quindi osservabili.

Per esempio, all’interno di una stella, verrebbero prodotti gravitoni in abbondanza. Una volta prodotti, questi scapperebbero facilmente nelle dimensioni in più, portando con sé energia e quindi raffreddando la stella in tempi molto più brevi di quelli effettivamente osservati. Questa catastrofe stellare può essere però evitata se si assumono dei valori un po’ più elevati per la costante gravitazionale (3+n)-dimensionale, G.

Ma gli effetti di gran lunga più spettacolari li riserverebbe la fisica dei collisori di particelle. A LHC, il collisore di protoni in costruzione al CERN, potrebbero venire prodotti nuovi stati, detti di Kaluza-Klein, associabili a particelle che “vivono” nelle nuove dimensioni e con una spettroscopia molto peculiare, e perfino veri e propri buchi neri.

Realtà o, come sembra temere Frank Wilczek in un recente articolo su Physics Today, allucinazioni d’alta montagna? Non ci resta che aspettare

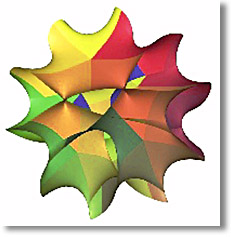
Fig. 1 Una rappresentazione dell’universo a molte dimensioni di Calabi-Yau, una possibile struttura prevista dalle teoria di superstringa

Fig. 2Due dimensioni “extra” arrotolate in forma di sfera

Fig. 3 Il pendolo di torsione utilizzato dall’esperimento Eötwash per la misura della legge di Newton a piccole distanze

Fig. 4 Paolo Conti, Matematica eleganza,smalto su tela, 2002