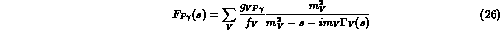Next: 7.2 Models for F.F.
Up: 7 Models for form
Previous: 7 Models for form
A general review on VMD and many of its results can be found in ref.
[1]. Here, we simply concentrate on the main formulae for
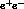 annihilations. In this case, the crucial point in the model is
the assumption that the blob in Fig.(1), connecting the intermediate
photon to the final hadronic state, reduces to a vector meson (or sum
over vector mesons) propagator(s). More precisely, the diagram is
assumed to contain a
annihilations. In this case, the crucial point in the model is
the assumption that the blob in Fig.(1), connecting the intermediate
photon to the final hadronic state, reduces to a vector meson (or sum
over vector mesons) propagator(s). More precisely, the diagram is
assumed to contain a  conversion vertex (with a coupling
given by
conversion vertex (with a coupling
given by 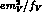 ), followed by the V-propagator and the final
V-decay vertex into f (with a
), followed by the V-propagator and the final
V-decay vertex into f (with a 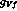 coupling constant). The
cross-section turns out to be
coupling constant). The
cross-section turns out to be
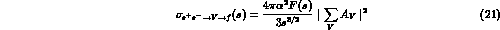
with the sum extending over the relevant V-mesons, F(s) being the final
phase space factor and
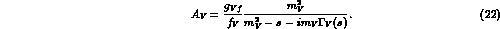
The values of the  couplings can be extracted from
couplings can be extracted from  data
[11] through
data
[11] through 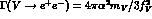 and are essentially compatible with the nonet symmetry and ideal
and are essentially compatible with the nonet symmetry and ideal
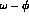 mixing predictions
mixing predictions  . For the various final states f, one has
. For the various final states f, one has
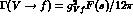 in such a way that the
in such a way that the
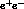 -cross section factorizes into a V-production and V-decay
factor. More explicitly, at a resonance peak, one has
-cross section factorizes into a V-production and V-decay
factor. More explicitly, at a resonance peak, one has

The particularization of the above formulae to the pseudoscalar form
factor case is extremely simple. For pions one has
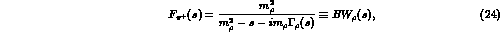
where the VMD relation  has been used. For
kaons one similarly obtains
has been used. For
kaons one similarly obtains
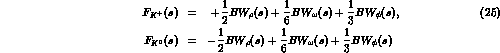
where the numerical coefficients follow from SU(3) Clebsch-Gordans and
quark charges. These F.F. satisfy the simple VMD relation 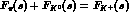 .
.
The above simple equations give a quite reasonable description of
pseudoscalar pair production below 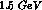 , thus showing the
adequacy of the naive VMD hypothesis. For a more accurate description
further details and fine tuning of parameters is required. This
proceeds in two main directions. One consists in extending the sum not
only to the lowest-lying V-mesons but also to their high-mass
recurrencies or radial excitations. Small improvements are then
obtained along the lines of refs. [18] [4] and
[14]. A second
line of improvement consists in introducing SU(3)-breaking effects as
described in detail in a next section [15]. The later are of
interest in Daphne, where
, thus showing the
adequacy of the naive VMD hypothesis. For a more accurate description
further details and fine tuning of parameters is required. This
proceeds in two main directions. One consists in extending the sum not
only to the lowest-lying V-mesons but also to their high-mass
recurrencies or radial excitations. Small improvements are then
obtained along the lines of refs. [18] [4] and
[14]. A second
line of improvement consists in introducing SU(3)-breaking effects as
described in detail in a next section [15]. The later are of
interest in Daphne, where 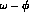 and
and 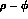 mixings (or,
equivalently, the precise quark content of the
mixings (or,
equivalently, the precise quark content of the  ) should be
accurately measured.
) should be
accurately measured.
The 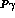 transition form factors are readily obtained in the VMD
context. Now one has
transition form factors are readily obtained in the VMD
context. Now one has
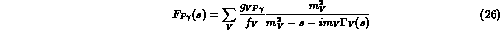
leading to an economical and reasonable description of the data. Again,
some improvements can be performed along the same lines as before.
Details can be found in refs. [16] and [15] in these
proceedings.



Next: 7.2 Models for F.F.
Up: 7 Models for form
Previous: 7 Models for form
Carlos E.Piedrafita
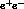 annihilations. In this case, the crucial point in the model is
the assumption that the blob in Fig.(1), connecting the intermediate
photon to the final hadronic state, reduces to a vector meson (or sum
over vector mesons) propagator(s). More precisely, the diagram is
assumed to contain a
annihilations. In this case, the crucial point in the model is
the assumption that the blob in Fig.(1), connecting the intermediate
photon to the final hadronic state, reduces to a vector meson (or sum
over vector mesons) propagator(s). More precisely, the diagram is
assumed to contain a  conversion vertex (with a coupling
given by
conversion vertex (with a coupling
given by 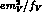 ), followed by the V-propagator and the final
V-decay vertex into f (with a
), followed by the V-propagator and the final
V-decay vertex into f (with a 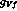 coupling constant). The
cross-section turns out to be
coupling constant). The
cross-section turns out to be
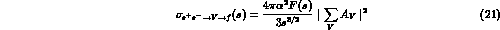
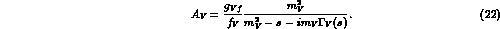
 couplings can be extracted from
couplings can be extracted from 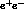 data
[
data
[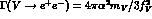 and are essentially compatible with the nonet symmetry and ideal
and are essentially compatible with the nonet symmetry and ideal
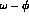 mixing predictions
mixing predictions  . For the various final states f, one has
. For the various final states f, one has
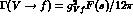 in such a way that the
in such a way that the
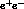 -cross section factorizes into a V-production and V-decay
factor. More explicitly, at a resonance peak, one has
-cross section factorizes into a V-production and V-decay
factor. More explicitly, at a resonance peak, one has

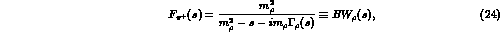
 has been used. For
kaons one similarly obtains
has been used. For
kaons one similarly obtains
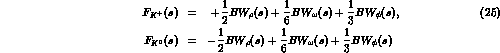
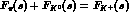 .
.
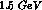 , thus showing the
adequacy of the naive VMD hypothesis. For a more accurate description
further details and fine tuning of parameters is required. This
proceeds in two main directions. One consists in extending the sum not
only to the lowest-lying V-mesons but also to their high-mass
recurrencies or radial excitations. Small improvements are then
obtained along the lines of refs. [
, thus showing the
adequacy of the naive VMD hypothesis. For a more accurate description
further details and fine tuning of parameters is required. This
proceeds in two main directions. One consists in extending the sum not
only to the lowest-lying V-mesons but also to their high-mass
recurrencies or radial excitations. Small improvements are then
obtained along the lines of refs. [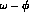 and
and 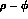 mixings (or,
equivalently, the precise quark content of the
mixings (or,
equivalently, the precise quark content of the  ) should be
accurately measured.
) should be
accurately measured.
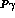 transition form factors are readily obtained in the VMD
context. Now one has
transition form factors are readily obtained in the VMD
context. Now one has