


Next: 1.1 Elastic Form Factors
Up: Chapter 9 Section 1
Previous: Chapter 9 Section 1
Low-energy 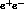 -machines are the ideal tool to investigate
the time-like region of the electromagnetic form factors (F.F.)
of low-mass hadrons, i.e., of the lowest spin mesonic and baryonic
states constructed only with u-, d- and s-quarks.
The initial
-machines are the ideal tool to investigate
the time-like region of the electromagnetic form factors (F.F.)
of low-mass hadrons, i.e., of the lowest spin mesonic and baryonic
states constructed only with u-, d- and s-quarks.
The initial 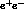 pair converts into an exclusive final
state containing two particles (A and
pair converts into an exclusive final
state containing two particles (A and 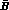 , with four-momenta p
and
, with four-momenta p
and 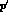 ) through the exchange of a virtual single-photon of squared
four-momentum
) through the exchange of a virtual single-photon of squared
four-momentum 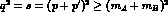 as shown in Fig.(1).
The amplitude associated to this process is
as shown in Fig.(1).
The amplitude associated to this process is
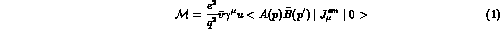
where the first factors contain the QED point-like vertex
and the photon propagator,
whereas the final one, written in terms of the hadronic
electromagnetic (e.m.) current and represented by the blob in
Fig.(1),
incorporates the effects of strong interactions and hadronic
structure in one or a few form factors, 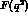 .
.
From the well-known conservation rules in both strong and e.m.
interactions, and the fact that we are exclusively considering
processes mediated by a single photon, the two-particle final
state is forced to have
the photonic quantum numbers too, i.e., J = 1, P = C = -1
and isospin I = 1 or 0. These quantum numbers can be achieved
either with A = B or with 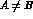 , thus allowing to distinguish
between ``elastic (or static)" form factors and ``transition (or
dynamical)" ones, as we now proceed to discuss.
, thus allowing to distinguish
between ``elastic (or static)" form factors and ``transition (or
dynamical)" ones, as we now proceed to discuss.
Carlos E.Piedrafita
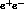 -machines are the ideal tool to investigate
the time-like region of the electromagnetic form factors (F.F.)
of low-mass hadrons, i.e., of the lowest spin mesonic and baryonic
states constructed only with u-, d- and s-quarks.
The initial
-machines are the ideal tool to investigate
the time-like region of the electromagnetic form factors (F.F.)
of low-mass hadrons, i.e., of the lowest spin mesonic and baryonic
states constructed only with u-, d- and s-quarks.
The initial 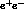 pair converts into an exclusive final
state containing two particles (A and
pair converts into an exclusive final
state containing two particles (A and 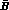 , with four-momenta p
and
, with four-momenta p
and 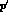 ) through the exchange of a virtual single-photon of squared
four-momentum
) through the exchange of a virtual single-photon of squared
four-momentum 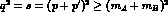 as shown in Fig.(1).
The amplitude associated to this process is
as shown in Fig.(1).
The amplitude associated to this process is
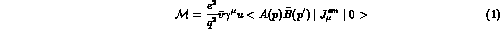
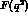 .
.
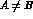 , thus allowing to distinguish
between ``elastic (or static)" form factors and ``transition (or
dynamical)" ones, as we now proceed to discuss.
, thus allowing to distinguish
between ``elastic (or static)" form factors and ``transition (or
dynamical)" ones, as we now proceed to discuss.