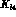 decays has been used so far for
three purposes:
decays has been used so far for
three purposes:
The chiral analysis of 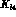 decays has been used so far for
three purposes:
decays has been used so far for
three purposes:
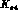 data from Ref. [53] allows one to make
predictions for the slope of the G form factor, for the total rates
in all the channels and for
the
data from Ref. [53] allows one to make
predictions for the slope of the G form factor, for the total rates
in all the channels and for
the 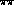 scattering lengths. These are given in Eq.
(5.85), in table 5.4 and in table 5.2, respectively.
scattering lengths. These are given in Eq.
(5.85), in table 5.4 and in table 5.2, respectively.
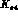 data allow one to test the large-
data allow one to test the large- prediction, see Eqs. (5.82) and (5.83).
prediction, see Eqs. (5.82) and (5.83).
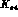 and
and 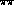 scattering data
allows the best determination of the coefficients
scattering data
allows the best determination of the coefficients 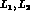 and
and  in the chiral Lagrangian, see (5.80).
in the chiral Lagrangian, see (5.80).
In the next generation of  decay experiments, there is the
opportunity to improve the phenomenology of
decay experiments, there is the
opportunity to improve the phenomenology of 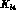 (see table
5.1):
(see table
5.1):
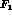 and
and 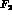 could be
inserted,
using the chiral representation solely to describe the small background effects
due to higher partial waves
could be
inserted,
using the chiral representation solely to describe the small background effects
due to higher partial waves 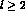 .
To be more precise, one would take for R and H the one-loop chiral
representation, whereas for G one writes
.
To be more precise, one would take for R and H the one-loop chiral
representation, whereas for G one writes
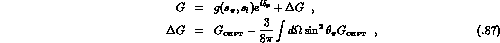
and similarly for F. The unknown amplitudes 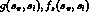 and the phases
and the phases 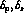 would then be determined from the data.
We have checked that, if the errors in the form factors determined in this
manner can be reduced by e.g. a factor 3
with respect to the
ones shown in (5.37), one could pin down particular combinations of
would then be determined from the data.
We have checked that, if the errors in the form factors determined in this
manner can be reduced by e.g. a factor 3
with respect to the
ones shown in (5.37), one could pin down particular combinations of
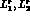 and
and 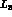 to considerably better precision than was shown above.
This is true independently of an eventual improvement in the theoretical
determination of the higher-order corrections in the form factor G -- which
is a theoretical challenge in any case.
to considerably better precision than was shown above.
This is true independently of an eventual improvement in the theoretical
determination of the higher-order corrections in the form factor G -- which
is a theoretical challenge in any case.
 parameter
parameter
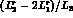 .
. 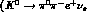 decays are mainly sensitive to
decays are mainly sensitive to 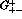 which in turn can be
used to pin down
which in turn can be
used to pin down  .
. 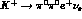 is mainly sensitive to
is mainly sensitive to 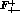 which contains
which contains 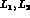 and
and
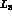 .)
.)
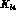 reactions with high
statistics could provide a cleaner separation of the various
isospin amplitudes.
reactions with high
statistics could provide a cleaner separation of the various
isospin amplitudes.
 has
been used [59] to determine the isoscalar S-wave
scattering length with the result
has
been used [59] to determine the isoscalar S-wave
scattering length with the result 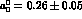 . This
value must be compared with the SU(2)
. This
value must be compared with the SU(2) SU(2) prediction
[77,78]
SU(2) prediction
[77,78] 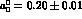 . Low-energy
. Low-energy 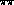 scattering is one of the few places where chiral symmetry allows
one to make a precise prediction within the framework of QCD. In
their article, Rosselet et al. comment about the discrepancy
between
scattering is one of the few places where chiral symmetry allows
one to make a precise prediction within the framework of QCD. In
their article, Rosselet et al. comment about the discrepancy
between 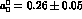 and the leading-order result
[79]
and the leading-order result
[79] 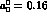 in the following manner: ``... it
appears that this prediction can be revised without any
fundamental change in current algebra or in the partial
conservation of axial-vector current [80,81]."
Today, we know that this is not the case: The standard picture of the
vacuum structure in QCD [82] would have to be revised,
should the central value
in the following manner: ``... it
appears that this prediction can be revised without any
fundamental change in current algebra or in the partial
conservation of axial-vector current [80,81]."
Today, we know that this is not the case: The standard picture of the
vacuum structure in QCD [82] would have to be revised,
should the central value 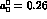 be
confirmed with a substantially smaller error. For recent work which
supports this scenario see the contribution of Knecht and Stern in this
Handbook [83].
be
confirmed with a substantially smaller error. For recent work which
supports this scenario see the contribution of Knecht and Stern in this
Handbook [83].
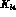 decays are -- at present [75] -- the only
available source of clean information on
decays are -- at present [75] -- the only
available source of clean information on 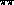 S-wave
scattering near threshold. We refer the reader to Ref.
[84] for a detailed analysis of the issue.
S-wave
scattering near threshold. We refer the reader to Ref.
[84] for a detailed analysis of the issue.