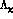
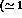 GeV).
The addition of higher dimensional multifermion interactions with increasing
powers of derivatives takes into account in a perturbative way the
nonlocality of the effective low energy action.
GeV).
The addition of higher dimensional multifermion interactions with increasing
powers of derivatives takes into account in a perturbative way the
nonlocality of the effective low energy action.
In the framework of effective fermion models à la Nambu-Jona Lasinio
for low energy hadronic interactions, the Quark-Resonance model [1]
can be thought of as a generalized ENJL [2] (see also chapter 1) model.
While the ENJL model only includes the lowest dimensional non-renormalizable
four fermion interaction terms, the Quark-Resonance (QR) Lagrangian
results from
the bosonization of the infinite tower of chiral invariant multiquark
effective interactions ordered by an expansion in inverse powers of
the ultraviolet cutoff 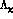
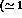 GeV).
The addition of higher dimensional multifermion interactions with increasing
powers of derivatives takes into account in a perturbative way the
nonlocality of the effective low energy action.
GeV).
The addition of higher dimensional multifermion interactions with increasing
powers of derivatives takes into account in a perturbative way the
nonlocality of the effective low energy action.
In section 2. the quark-resonance Lagrangian is constructed up to
including 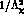 terms, which are next-to-leading in the
inverse cutoff expansion and leading in the
terms, which are next-to-leading in the
inverse cutoff expansion and leading in the 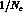 expansion.
All meson SU(3) flavour octet quantum numbers are included:
the pseudoscalar mesons
expansion.
All meson SU(3) flavour octet quantum numbers are included:
the pseudoscalar mesons 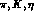 , the vector, axial, scalar and
pseudoscalar resonances.
In section 3. two parameters of the leading vector resonance chiral
effective Lagrangian are derived, including
, the vector, axial, scalar and
pseudoscalar resonances.
In section 3. two parameters of the leading vector resonance chiral
effective Lagrangian are derived, including 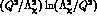 corrections to the leading logarithmic ENJL contribution:
the coupling of the vector resonance to the external vector current
and the vector mass. They enter the calculation of the vector two point
function, which is studied in section 4 in the chiral limit; the
numerical relevance of
corrections to the leading logarithmic ENJL contribution:
the coupling of the vector resonance to the external vector current
and the vector mass. They enter the calculation of the vector two point
function, which is studied in section 4 in the chiral limit; the
numerical relevance of 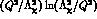 in the
intermediate
in the
intermediate 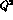 region is shown through the comparison with
experimental data.
region is shown through the comparison with
experimental data.