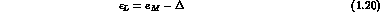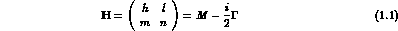
truecm
The hamiltonian of the neutral Kaon system, in the particle rest frame, is a complex, 2x2 matrix:
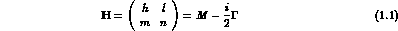
We are in the basis:
h, l, m, n are complex numbers (so that H depends upon 8 real
parameters), and M and 
are hermitian matrices.
The sign of the antihermitian part of H is determined by the requirement
that it must lead to exponential damping of the wave-function, for
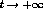. With the sign given in Eq. (1.1), the time-dependent
factor of the wave-function is: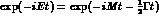 
,
which is correct, provided that 
has non-negative eigenvalues.
We shall also write:
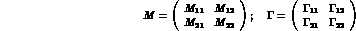
truecm
Symmetries. truecm CP:
T :
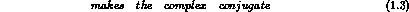
It follows (
Pauli matrices):
CP:
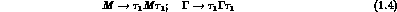
T:
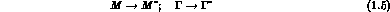
If we develop both M and 
in the basis of the Pauli matrices plus the
identity,
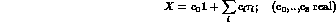
we are led to the following Table, which gives the sign taken by each component under CP, T and CPT transformations. truecm Tab.1
We recover the familiar result that CPT implies equal diagonal elements.
Also, CP conservation implies CPT conservation (unlike in 
decay
amplitudes, see below).
There is some freedom to redefine the phases of the states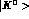 
and
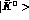. Strangeness is conserved by strong and e.m. interactions, so we
can make the change:
i.e.:
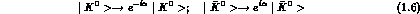
In the new basis, the CP transformation is not given by (1.2)
anymore, so that the matrix H needs not satisfy the rules given above,
even if CP is conserved. All this amounts to say that CP is conserved
if and only if there exists a change
of phase of the form (1.6) such that, in the new basis, M and 
have
vanishing components along 
and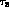 
. This happens when 
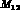and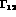 
have the same phase. We conclude that the
phase-invariant condition for CP conservation is:
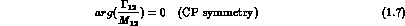
Diagonal elements are not affected by the phase change, so that the condition for CPT symmetry is always:
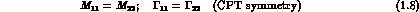
Eigenvalue equation:
leads to:
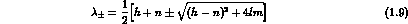
note: 
.
Eigenvectors:
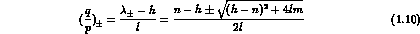
The identification of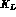 
and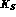 
states is obtained by going to the
symmetric limit of exact CP (and CPT). In this limit, see (1.7) and (1.8):
so that:
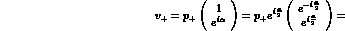
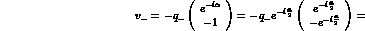
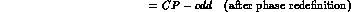
Therefore, by continuity, we identify:
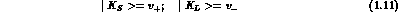
Conventionally, eigenvectors are written in terms of two
complex numbers,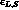 
, defined by:
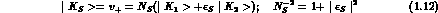
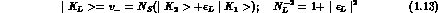
with:
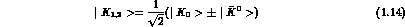
The Hamiltonian matrix is determined by 8 real parameters, which we can
substitute with the 2 complex eigenvalues and the 2 complex mixing parameters,
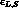. The relevant formulae are:
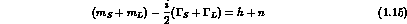
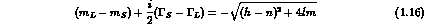
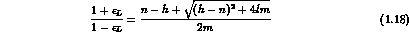
In the CPT symmetric limit, h=n and there is only one mixing parameter,
, determined by:
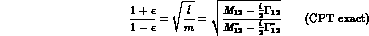
To keep contact with the CPT-invariant limit, the 
's are conveniently
written as:
