 NE
NEINFN - Laboratori Nazionali di Frascati, May 1995
From: The Second DAFNE Physics Handbook
Chapter 12: Nuclear Physics with Kaons
Eds. L. Maiani, G. Pancheri, N. Paver
Supported by the INFN, by the EC under the HCM contract number CHRX-CT920026 and by the authors home institutions.
 NE
NE
cm
P. M. Gensini
Dip. di Fisica dell´` Universita di Perugia,
and INFN, Sezione di Perugia,
Perugia, Italy
 NE can be expected to offer over them.
Interactions in deuterium and other light nuclei will be only briefly
mentioned, and only in those respects touching directly upon the more
``elementary'' aspects of kaon--nucleon interactions.
NE can be expected to offer over them.
Interactions in deuterium and other light nuclei will be only briefly
mentioned, and only in those respects touching directly upon the more
``elementary'' aspects of kaon--nucleon interactions.
cm 1. Introduction. 0.3truecm
DA NE is expected to produce, with ``standard'' assumptions about
luminosity and cross sections, about
NE is expected to produce, with ``standard'' assumptions about
luminosity and cross sections, about 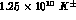 's and
's and
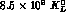 's per year of operation, considering a conventional
``Snowmass year'' of
's per year of operation, considering a conventional
``Snowmass year'' of 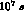 . With a detector of KLOE's size one can thus
expect to observe up to millions of interactions per year,
even in the low--density gas (mostly helium at atmospheric pressure)
filling its fiducial volume.
. With a detector of KLOE's size one can thus
expect to observe up to millions of interactions per year,
even in the low--density gas (mostly helium at atmospheric pressure)
filling its fiducial volume.
A first question has thus to be answered: do these events contain useful
physics to be worth recording and interpreting? One could even go further
and envisage using DA NE as a source of high--resolution (
NE as a source of high--resolution (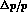 of respectively
of respectively 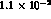 for
for 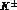 's and
's and 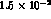 for
for 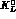 's), low--momentum kaons (
's), low--momentum kaons (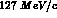 for the former, minus the
losses in the matter along the kaon path from DA
for the former, minus the
losses in the matter along the kaon path from DA NE's beam--beam
interaction region to the point where it interacts in the detector, and
NE's beam--beam
interaction region to the point where it interacts in the detector, and
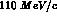 for the latter), to measure with a dedicated detector
KN and
for the latter), to measure with a dedicated detector
KN and 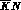 interactions, e.g. in a toroidal volume
filled with gaseous
interactions, e.g. in a toroidal volume
filled with gaseous 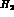 or
or 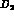 , and possibly also with heavier--element,
gaseous (i.e. low--density) targets.
, and possibly also with heavier--element,
gaseous (i.e. low--density) targets.
The machine has thus the ability to explore a small kinematical region
(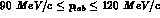 ), very little investigated in
the past:
only few bubble--chamber
), very little investigated in
the past:
only few bubble--chamber 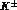 experiments in hydrogen (and
deuterium)
experiments in hydrogen (and
deuterium)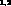 plus very few data points on
plus very few data points on 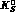 regeneration
regeneration exist,
all with extremely low statistics and more than a decade old (the last
experiment
exist,
all with extremely low statistics and more than a decade old (the last
experiment to cover this region was carried out in the second half
of the seventies by the TST Collaboration at the hydrogen bubble chamber
in NIMROD's low--energy kaon beam). Since in dispersive calculations
of low--energy parameters for KN interactions (
to cover this region was carried out in the second half
of the seventies by the TST Collaboration at the hydrogen bubble chamber
in NIMROD's low--energy kaon beam). Since in dispersive calculations
of low--energy parameters for KN interactions (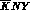 and
and 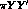 coupling constants, scattering lengths,
coupling constants, scattering lengths,  --terms) the bulk of the
uncertainties comes from the integrals over the unphysical regions, for
whose description one must extrapolate data analyses for quite an energy
range, down from the physical region well above the
charge--exchange threshold, DA
--terms) the bulk of the
uncertainties comes from the integrals over the unphysical regions, for
whose description one must extrapolate data analyses for quite an energy
range, down from the physical region well above the
charge--exchange threshold, DA NE, as the cleanest, lowest--energy kaon
source ever built, can be expected to make substantial improvements
over our present knowledge of those parameters.
NE, as the cleanest, lowest--energy kaon
source ever built, can be expected to make substantial improvements
over our present knowledge of those parameters.
The following sections are therefore dedicated to
illustrating the details (and the limitations) of present--day
information on low--energy kaon--nucleon
physics, spotlighting those points which still await being clarified,
and where DA NE can be expected to improve. Being the
phenomenology in this case more complex than in the (strictly related)
pion--nucleon one, we shall start almost from scratch.
NE can be expected to improve. Being the
phenomenology in this case more complex than in the (strictly related)
pion--nucleon one, we shall start almost from scratch.
We shall also take the liberty of not going into the details of models,
in particular for the spectroscopic classification of the
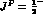 , S--wave resonance
, S--wave resonance 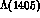 : data are still
so scarce, after more than two decades of studies,
that any interpretation of such a state is to be
regarded as purely conjectural
: data are still
so scarce, after more than two decades of studies,
that any interpretation of such a state is to be
regarded as purely conjectural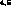 .
.
1.0truecm
2. Amplitude formalism for two--body KN and 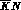 interactions.
0.3truecm
interactions.
0.3truecm
Any 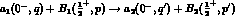 process is most economically described in the centre--of--mass (c.m.) frame
by two amplitudes,
process is most economically described in the centre--of--mass (c.m.) frame
by two amplitudes, 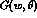 and
and 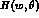 , when the T--matrix element
, when the T--matrix element
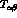 is expressed in terms of the two--component Pauli spinors
is expressed in terms of the two--component Pauli spinors
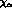 and
and 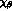 (respectively for the final and initial
(respectively for the final and initial
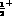 baryons) as
baryons) as 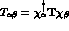 , where
, where
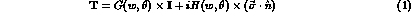
and  defines the normal to the scattering plane
defines the normal to the scattering plane .
.
These c.m. amplitudes have a simple expansion in the partial waves
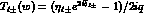 ,
given by
,
given by
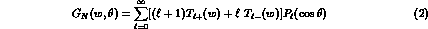
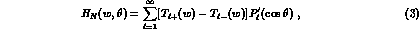
where the subscript N indicates that only the purely nuclear part of the interaction has been considered.
To describe adequately the data, the amplitudes must also include electromagnetism and can be rewritten as
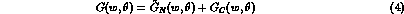
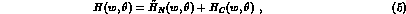
where the tilded nuclear amplitudes differ from the untilded ones only in the
(generally complex) Coulomb shifts 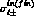 having
been applied to each partial wave
having
been applied to each partial wave  , namely when
, namely when
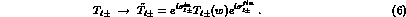
The one--photon--exchange amplitudes 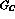 and
and 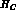 (of course
absent for charge-- and/or strangeness--exchange processes, but present at
(of course
absent for charge-- and/or strangeness--exchange processes, but present at
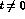 for
for 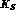 regeneration, which can also go via one--photon
exchange) can be expressed in terms of the Dirac nucleon form factors
as
regeneration, which can also go via one--photon
exchange) can be expressed in terms of the Dirac nucleon form factors
as (M and m indicate respectively the baryon and meson masses
in the inital state: for final states all quantities will be primed)
(M and m indicate respectively the baryon and meson masses
in the inital state: for final states all quantities will be primed)
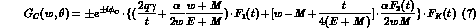
and
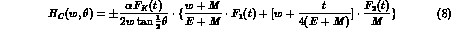
for the interactions of (respectively)  with nucleons, while for
with nucleons, while for
 regeneration one has to change the sign of the isovector part
regeneration one has to change the sign of the isovector part
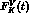 of the kaon form factor
of the kaon form factor 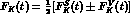 , the plus sign holding for charged kaons, the minus for the neutral ones.
Here
, the plus sign holding for charged kaons, the minus for the neutral ones.
Here 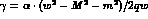 and the Coulomb phase
and the Coulomb phase
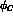 is defined as
is defined as
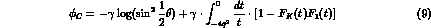
for charged kaons scattering on protons, while it reduces to
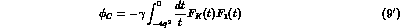
for processes involving 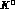 's and/or neutrons.
's and/or neutrons.
We have denoted with w and  respectively the total energy
and the scattering angle in the c.m. frame,
respectively the total energy
and the scattering angle in the c.m. frame, 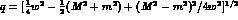 is the c.m. momentum (in the
initial state: for inelastic processes, including charge exchange, we shall
indicate final--state kinematical quantities with primes), E the total
energy of the baryon in the c.m. frame,
is the c.m. momentum (in the
initial state: for inelastic processes, including charge exchange, we shall
indicate final--state kinematical quantities with primes), E the total
energy of the baryon in the c.m. frame, 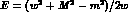 , and t
the squared momentum--transfer,
, and t
the squared momentum--transfer, 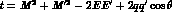 .
We shall also use the laboratory--frame, initial--meson momentum
.
We shall also use the laboratory--frame, initial--meson momentum 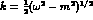 and energy
and energy  , related to the
c.m. total energy via
, related to the
c.m. total energy via 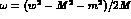 , and, besides t,
the two other
Mandelstam variables
, and, besides t,
the two other
Mandelstam variables 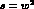 and u, the square of the c.m. total energy
for the crossed channel
and u, the square of the c.m. total energy
for the crossed channel 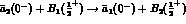 , obeying on the mass shell the indentity
, obeying on the mass shell the indentity 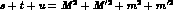 .
.
In terms of the amplitudes G and H the c.m. differential cross
sections for an unpolarized target (surely the case for experiments to be
carried on at DA NE) take the simple form
NE) take the simple form
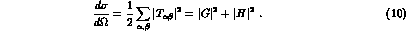
The other observables possibly accessible at DA NE, in the
strangeness--exchange processes
NE, in the
strangeness--exchange processes 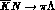 and
and
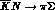 , are the polarizations
, are the polarizations 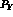 (
(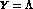 or
or
 ) of the final hyperons, measurable through the asymmetries
) of the final hyperons, measurable through the asymmetries  of their weak nonleptonic decays
of their weak nonleptonic decays 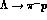 or
or 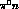 , for both of
which we have an asymmetry
, for both of
which we have an asymmetry 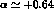 , and
, and 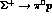 for
which the asymmetry is
for
which the asymmetry is 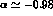 , while there is very little
chance to be able to use the neutron decay modes
, while there is very little
chance to be able to use the neutron decay modes 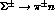 ,
which have the very small asymmetries
,
which have the very small asymmetries 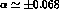 ; we have for
these quantities
; we have for
these quantities
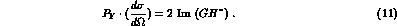
Note that, for an 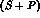 --wave parametrization (fully adequate at such low
momenta), while the integrated cross sections depend only
quadratically on the P--waves, both the first Legendre coefficients of the
differential cross sections
--wave parametrization (fully adequate at such low
momenta), while the integrated cross sections depend only
quadratically on the P--waves, both the first Legendre coefficients of the
differential cross sections
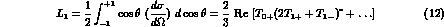
and the polarizations
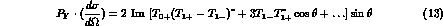
are essentially linear in the small P--wave contributions, and give
two complementary pieces of information on these latter.
It is perhaps not useless to remind
the reader that the low statistics of the experiments, performed only up
to the late seventies, have not been enough to determine any of these
parameters, yielding only very inaccurate (and utterly useless)
determinations of
of 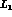 for the charged--hyperon production channels.
for the charged--hyperon production channels.
We shall now devote the last part of this section to show explicitly why
this absence of direct information on the low--energy behaviour of the
P--waves has been a serious shortcoming for 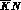 amplitude
analyses. Remember that we know, from production experiments, that the
I = 1, S = -1
amplitude
analyses. Remember that we know, from production experiments, that the
I = 1, S = -1 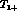 partial wave resonates below threshold at a
c.m. energy around
partial wave resonates below threshold at a
c.m. energy around 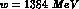 , the mass of the neutral, isovector
member of the
, the mass of the neutral, isovector
member of the 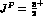 decuplet
decuplet , but beyond this piece
of information P--waves
are practically unmeasured up to momenta above
, but beyond this piece
of information P--waves
are practically unmeasured up to momenta above 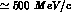 .
.
One has to turn from the Pauli amplitudes G and H to the invariant
amplitudes 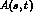 and
and 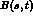 , defined in term of four--component Dirac
spinors as
, defined in term of four--component Dirac
spinors as
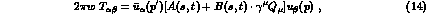
where 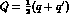 , the average between incoming-- and
outgoing--meson c.m. four--momenta: these amplitudes obey simple
crossing relations and are free of kinematical
singularities, so that they are the ones to be used, rather than G and H,
for any analytical extrapolation purpose; it is also customary to use the
combination
, the average between incoming-- and
outgoing--meson c.m. four--momenta: these amplitudes obey simple
crossing relations and are free of kinematical
singularities, so that they are the ones to be used, rather than G and H,
for any analytical extrapolation purpose; it is also customary to use the
combination 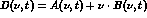 , where
, where 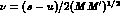 , which has the same properties as
, which has the same properties as 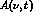 under crossing,
and furthermore, for elastic scattering, obeys the optical theorem
in the simple form
under crossing,
and furthermore, for elastic scattering, obeys the optical theorem
in the simple form
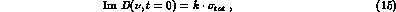
where of course all electromagnetic effects must be subtracted on both sides.
One can rewrite A and B in terms of G and H, and thus reexpress them
through the partial waves 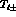 , by projecting eq. (14) on the
different spin states (polarized perpendicularly to the scattering
plane) and obtain in the most general kinematics
, by projecting eq. (14) on the
different spin states (polarized perpendicularly to the scattering
plane) and obtain in the most general kinematics
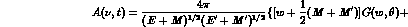
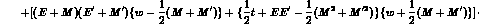
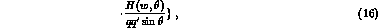
0.3truecm and
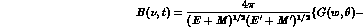
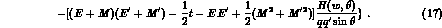
0.3truecm
Considering for sake of simplicity forward elastic scattering only, the amplitudes become, leaving out D-- and higher waves,
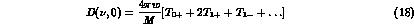
and
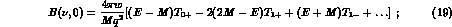
introducing the (complex) scattering lengths 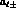 and (complex)
effective ranges
and (complex)
effective ranges 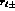 one can expand up to
one can expand up to 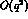 the partial
waves close to threshold, and obtain for the forward D amplitudes
the partial
waves close to threshold, and obtain for the forward D amplitudes
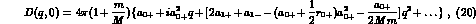
dominated by the S--waves, while for the B amplitudes the same approximations give
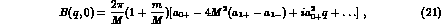
where the factor 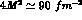 enhances considerably the
contributions by the low--energy P--waves (virtually unkown), rendering
practically useless the unsubtracted dispersion relation for the better
converging B amplitudes, so important for the
enhances considerably the
contributions by the low--energy P--waves (virtually unkown), rendering
practically useless the unsubtracted dispersion relation for the better
converging B amplitudes, so important for the  case in fixing
accurately the values of the coupling constant
case in fixing
accurately the values of the coupling constant 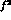 and of the S--wave
scattering lengths
and of the S--wave
scattering lengths .
.
1.0truecm 3. The Coulomb corrections and the kaonic hydrogen ``puzzle''. 0.3truecm
The Coulomb shifts 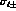 can be separated into the real, purely
Coulomb phases
can be separated into the real, purely
Coulomb phases 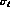 and the complex Coulomb corrections
and the complex Coulomb corrections
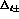 ,
,
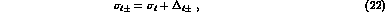
where 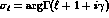 to lowest
order in
to lowest
order in  , and the Coulomb corrections
, and the Coulomb corrections 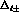 have to be
explicitly computed from a first--order ``ansatz'' on the purely nuclear
interaction. They have been computed in a dispersion--relation formalism by
Tromborg, Waldenstrøm and Øverbø
have to be
explicitly computed from a first--order ``ansatz'' on the purely nuclear
interaction. They have been computed in a dispersion--relation formalism by
Tromborg, Waldenstrøm and Øverbø for the
for the  case: the same
formalism
case: the same
formalism could in principle be extended (but has not been up to now) also
to the KN and
could in principle be extended (but has not been up to now) also
to the KN and 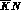 ones.
ones.
Since this method (as the other methods as well) uses a ``reference'' strong
interaction, minor corrections remain to be applied to the observed
phases 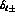 and elasticities
and elasticities 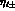 , to extract their
purely nuclear parts
, to extract their
purely nuclear parts ; a way of removing them efficiently has been
devised by the Karlsruhe--Helsinki group: it consists in starting from a
(preliminary) set of phase shifts, (i) calculating from them the corrections
in the above--mentioned dispersive formalism
; a way of removing them efficiently has been
devised by the Karlsruhe--Helsinki group: it consists in starting from a
(preliminary) set of phase shifts, (i) calculating from them the corrections
in the above--mentioned dispersive formalism , then (ii) the changes in
the observables brought about by these latter, and finally (iii) correcting
the data for these effects and (iv) starting the phase--shift analysis all
over again, this time from the ``corrected data''. This procedure has turned
out to be both self--consistent and fast
, then (ii) the changes in
the observables brought about by these latter, and finally (iii) correcting
the data for these effects and (iv) starting the phase--shift analysis all
over again, this time from the ``corrected data''. This procedure has turned
out to be both self--consistent and fast .
.
Of course, the accuracy of a dispersive approach is limited by the
overall accuracy of the experimental data, from which the ``reference''
interaction is extracted, and particularly by that of the low--energy ones,
which in the 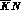 interaction is dominated by the very low
statistics of the most accurate -- and recent -- experiment
interaction is dominated by the very low
statistics of the most accurate -- and recent -- experiment .
.
As an alternative to the above dispersive approach , one can describe
the scattering and production processes by either
a Schrödinger
, one can describe
the scattering and production processes by either
a Schrödinger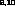 or a
Klein--Gordon
or a
Klein--Gordon multichannel wave equation, with both Coulomb and
strong--interaction potentials; such formalisms have the advantage, when
continuing the c.m. momentum q of the
multichannel wave equation, with both Coulomb and
strong--interaction potentials; such formalisms have the advantage, when
continuing the c.m. momentum q of the 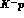 system from the real to the
imaginary axis, of predicting at the same time the hadronic level shifts and
widths for the kaonic--hydrogen atomic levels, present as an infinite number
of poles just below the elastic threshold in every partial wave, having the
threshold as an accumulation point.
system from the real to the
imaginary axis, of predicting at the same time the hadronic level shifts and
widths for the kaonic--hydrogen atomic levels, present as an infinite number
of poles just below the elastic threshold in every partial wave, having the
threshold as an accumulation point.
Such an approach is preferable when working at very low momenta, in absence of
previous experimental information of comparable quality, which is the case for
the foreseeable KN and 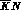 experiments to be carried out at
DA
experiments to be carried out at
DA NE. We shall in the following discuss in detail only the relatively
less know Klein--Gordon formalism, leaving out the Schrödinger one, whose
details are easily workable out, following e.g. the papers listed in reference
(10) as a guideline.
NE. We shall in the following discuss in detail only the relatively
less know Klein--Gordon formalism, leaving out the Schrödinger one, whose
details are easily workable out, following e.g. the papers listed in reference
(10) as a guideline.
The advantage of the Klein--Gordon formaliam over the Schrödinger one lies
mainly in the fact that the fine structure of mesic atoms is clearly
(and directly)
produced by the former but not by the latter: one would thus be tempted to use
it also to calculate the Coulomb modifications to the scattering amplitudes,
particularly in the low--energy region considered here, where both formalisms
give reasonable approximations to the true kinematics of the two--particle
system. We have indeed, for the c.m. kinetic energy 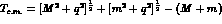 , the approximations
, the approximations 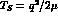 -- with the reduced mass
-- with the reduced mass 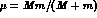 -- for the Schrödinger
equation, and
-- for the Schrödinger
equation, and 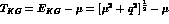 for the
Klein--Gordon one, both differing from each other and from
for the
Klein--Gordon one, both differing from each other and from 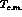 at
O(
at
O(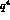 ) only.
) only.
However, to include an interaction with all the good symmetry properties expected for pseudoscalar mesons interacting with a baryonic ``source'', a Klein--Gordon equation has to possess at least a four--vector and a scalar term (being concerned mostly with the S--waves, we shall neglect for the moment the tensor part of the interaction), of the form (in the ``static limit'')
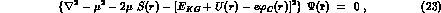
where the effective potentials 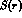 and
and 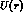 (real in the elastic,
single--channel case) are respectively even and odd under C--parity
conjugation of the meson fields (in a multi--channel case, such as the one we
are studying,
(real in the elastic,
single--channel case) are respectively even and odd under C--parity
conjugation of the meson fields (in a multi--channel case, such as the one we
are studying, 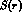 and
and 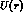 will be real, nondiagonal matrices, and
will be real, nondiagonal matrices, and
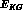 and
and 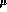 diagonal ones, of dimension
diagonal ones, of dimension 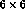 for
for 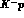 and
and
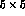 for
for 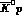 , and the product
, and the product 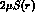 will have to
be replaced by the anticommutator
will have to
be replaced by the anticommutator 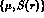 ): they can be separated only
if data on both the s-- and u--channel reactions are available
at the same c.m. energy, which is clearly not the case for the
pion--hyperon channels, since the processes
): they can be separated only
if data on both the s-- and u--channel reactions are available
at the same c.m. energy, which is clearly not the case for the
pion--hyperon channels, since the processes 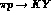 can be accessed
only at c.m. energies above
can be accessed
only at c.m. energies above 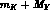 , well above the
, well above the 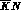 c.m.
energy available at DA
c.m.
energy available at DA NE, below 1442 MeV for
NE, below 1442 MeV for 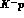 (and of only 1444
MeV for
(and of only 1444
MeV for 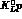 ).
).
One has therefore to abandon the real potentials for complex ones, reducing
oneself to treat with the Klein--Gordon equation (23) only the two, coupled
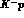 and
and 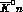 channels: however, one ambiguity is still left,
in the separation of the absorption effects from the neglected
channels: however, one ambiguity is still left,
in the separation of the absorption effects from the neglected 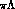 and
and 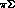 channels between the two potentials
channels between the two potentials 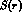 and
and 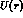 . This
ambiguity could be resolved
. This
ambiguity could be resolved , under the reasonable
assumption of an energy
dependence of the potentials
, under the reasonable
assumption of an energy
dependence of the potentials as gentle as expected from forward
dispersion relations and the absence of any dynamical effect apart from the
as gentle as expected from forward
dispersion relations and the absence of any dynamical effect apart from the
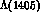 S--wave resonance below threshold
S--wave resonance below threshold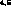 ,
if the energy shift
and width of the ground state for the
,
if the energy shift
and width of the ground state for the 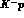 atomic system had been actually
measured: the three experiments performed in the late seventies and early
eighties on this system
atomic system had been actually
measured: the three experiments performed in the late seventies and early
eighties on this system have been widely quoted as to report
attractive hadronic shifts (and small widths), contrary to all
reasonable expectations
have been widely quoted as to report
attractive hadronic shifts (and small widths), contrary to all
reasonable expectations , but in fact none of the three has produced
convincing evidence for the identification of the X--ray transitions they
claim having observed as lines belonging to the K--series of the
, but in fact none of the three has produced
convincing evidence for the identification of the X--ray transitions they
claim having observed as lines belonging to the K--series of the 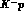 atomic
system. The only experiment having an acceptable signal--to--background ratio
(the first one conducted by Davies et al.
atomic
system. The only experiment having an acceptable signal--to--background ratio
(the first one conducted by Davies et al. in the same beam--line
of the TST Collaboration experiment
in the same beam--line
of the TST Collaboration experiment at NIMROD), observed only one
clear transition, which could well have been the
at NIMROD), observed only one
clear transition, which could well have been the 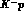 K
K line and
not the K
line and
not the K they claimed it to be (see the comments about this
problem in both reviews listed in reference (16)).
For the interpretation of the
they claimed it to be (see the comments about this
problem in both reviews listed in reference (16)).
For the interpretation of the 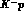 X--ray
lines the evaluation of their intensities is essential: a recent cascade
calculation has been performed by Reifenröther and Klempt
X--ray
lines the evaluation of their intensities is essential: a recent cascade
calculation has been performed by Reifenröther and Klempt . A new
experiment, which expects to achieve a much better signal--to--background
ratio, is presently under way at KEK
. A new
experiment, which expects to achieve a much better signal--to--background
ratio, is presently under way at KEK , and studies on the possibility of
a kaonic hydrogen experiment at DA
, and studies on the possibility of
a kaonic hydrogen experiment at DA NE must be seriously considered, for
this measurement will be complementary to, if not substitutive of,
a conventional beam--target experiment
such as the KEK one, due to the completely different nature in the possible
X-ray backgrounds.
NE must be seriously considered, for
this measurement will be complementary to, if not substitutive of,
a conventional beam--target experiment
such as the KEK one, due to the completely different nature in the possible
X-ray backgrounds.
The above ambiguity is not as serious an obstacle as it might appear at first
glance: the ``strong potentials'' 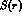 and
and 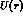 are usually assumed to
have a simple, predetermined r--dependence (with Rasche
and Woolcock
are usually assumed to
have a simple, predetermined r--dependence (with Rasche
and Woolcock we prefer square wells
we prefer square wells ,
, 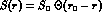 and
and 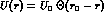 , since these yield very simple, analytic ``inner'' and
``outer'' solutions, i.e. respectively Bessel and Kummer (or Whittaker)
functions, once
, since these yield very simple, analytic ``inner'' and
``outer'' solutions, i.e. respectively Bessel and Kummer (or Whittaker)
functions, once 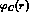 is substituted by its average value inside the
square well, and vacuum polarization is neglected at this stage, and later
treated as a small perturbation, though this requires some particular
care
is substituted by its average value inside the
square well, and vacuum polarization is neglected at this stage, and later
treated as a small perturbation, though this requires some particular
care in normalising the Klein--Gordon wavefunctions, with respect to
the Schrödinger ones), and the ambiguity reduces then to a single free
parameter, e.g. the ratio
in normalising the Klein--Gordon wavefunctions, with respect to
the Schrödinger ones), and the ambiguity reduces then to a single free
parameter, e.g. the ratio 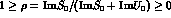 (since unitarity dictates both kind of
potentials, when absorptive, to have a negative imaginary part). The
calculation can now go on along the same lines as the Helsinki--Karlsruhe one
( modulo the different algorithms): one can start from an ``initial'' set
of phases, (i) turn them into a pair of potentials S, U, (ii) compute the
new corrections, (iii) use these latter to extract new phases, and (iv) start
again from the point (i) till input and output differ by less than a small,
pre--fixed amount.
(since unitarity dictates both kind of
potentials, when absorptive, to have a negative imaginary part). The
calculation can now go on along the same lines as the Helsinki--Karlsruhe one
( modulo the different algorithms): one can start from an ``initial'' set
of phases, (i) turn them into a pair of potentials S, U, (ii) compute the
new corrections, (iii) use these latter to extract new phases, and (iv) start
again from the point (i) till input and output differ by less than a small,
pre--fixed amount.
The procedure relies, rather than on cumbersome integrations (as in the
dispersive approach), on well known analytic functions, most of which if not
all already available in software packages, easy to adapt to the case under
study; the same software, after extrapolation of the potentials to threshold
through a reasonably small correction (q in the region covered by
DA NE's
NE's 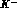 's goes from about 59 to about 78
's goes from about 59 to about 78 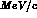 only), since it
contains automatically the Deser--Goldberger--Baumann--Thirring formula for
the hadronic shifts and widths
only), since it
contains automatically the Deser--Goldberger--Baumann--Thirring formula for
the hadronic shifts and widths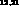 , can also produce, mutatis
mutandis, accurate predictions for shifts and widths of the
, can also produce, mutatis
mutandis, accurate predictions for shifts and widths of the 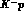 1s (and
Np, once the P--waves are determined as well) atomic states, and therefore
for the whole K--series, for any chosen set of the only two free
parameters left, i.e. the ratio
1s (and
Np, once the P--waves are determined as well) atomic states, and therefore
for the whole K--series, for any chosen set of the only two free
parameters left, i.e. the ratio 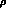 and the square--well radius
and the square--well radius 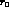 , to
be varied at most from once to twice the r.m.s. charge radius of the proton
(or up and down a
, to
be varied at most from once to twice the r.m.s. charge radius of the proton
(or up and down a 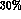 around
around 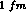 ).
).
1.0truecm
4. Open channels and baryon spectroscopy at DA NE.
0.3truecm
NE.
0.3truecm
As mentioned above, in the momentum region which could be explored by the
kaons coming from the decays of a  --resonance formed at rest in an
--resonance formed at rest in an 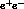 collision, we have only data from low--statistics experiments, mostly
hydrogen bubble--chamber ones on
collision, we have only data from low--statistics experiments, mostly
hydrogen bubble--chamber ones on 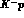 (and
(and 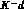 ) interactions
) interactions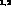 (dating from the early sixties trough the late seventies), plus scant data
from
(dating from the early sixties trough the late seventies), plus scant data
from 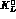 interactions and
interactions and 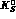 regeneration, mostly on hydrogen
regeneration, mostly on hydrogen .
.
The channels, open at a laboratory energy 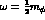 (for
(for
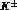 's to obtain the exact value of
's to obtain the exact value of  one has to include their
energy losses through ionization as well), are tabulated below for
interactions with free protons and neutrons, together with their
threshold energies
one has to include their
energy losses through ionization as well), are tabulated below for
interactions with free protons and neutrons, together with their
threshold energies 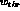 (in MeV), strangeness and isospin(s).
We do not list
(in MeV), strangeness and isospin(s).
We do not list 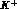 --initiated processes, which are (apart from charge
exchange) purely elastic in this energy region.
--initiated processes, which are (apart from charge
exchange) purely elastic in this energy region.
For interactions in hydrogen, the c.m. energy available for each final
state is limited by momentum conservation to the initial total c.m. energy,
equal (neglecting energy losses) to 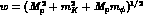 ,
or
,
or 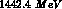 for incident
for incident 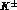 's and
's and 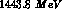 for incident
for incident
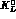 's. Energy losses for charged kaons can be exploited (using the inner
parts of the detector as a ``moderator'') to explore
's. Energy losses for charged kaons can be exploited (using the inner
parts of the detector as a ``moderator'') to explore 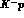 interactions in a
limited momentum range, possibly down to and below
the charge--exchange threshold
at
interactions in a
limited momentum range, possibly down to and below
the charge--exchange threshold
at 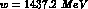 , corresponding to a
, corresponding to a 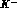 laboratory momentum of about
laboratory momentum of about
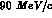 .
.
For interactions in deuterium (or in heavier nuclei), momentum can be carried
away by ``spectator'' nucleons, and one can explore each inelastic channel
from the highest available energy down to threshold. The possibility of
reaching energies below the 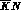 threshold is particularly
desirable, since the
threshold is particularly
desirable, since the 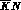 unphysical region contains two
resonances
unphysical region contains two
resonances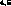 , the I = 0,
S--wave
, the I = 0,
S--wave 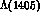 and the I = 1,
and the I = 1, 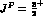 P--wave
P--wave 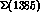 , observed mostly in production
experiments (and, in the first case, with very limited statistics
, observed mostly in production
experiments (and, in the first case, with very limited statistics ), so
that the information on their couplings to the
), so
that the information on their couplings to the 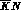 channel relies
entirely on extrapolations below threshold of the analyses of the
low--energy data. The coupling of the
channel relies
entirely on extrapolations below threshold of the analyses of the
low--energy data. The coupling of the 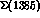 to the
to the 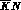 channel, for instance, can at present be determined only via forward
dispersion relations involving the total sum of data collected at
channel, for instance, can at present be determined only via forward
dispersion relations involving the total sum of data collected at 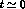 , but with uncertainties which are, at their best, still of the
order of 50% of the value expected from flavour--
, but with uncertainties which are, at their best, still of the
order of 50% of the value expected from flavour--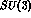 symmetry
symmetry ; as
for the
; as
for the 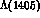 , even its spectroscopic classification is still an
open problem, vis--à--vis the paucity and (lack of) quality of the
best available data
, even its spectroscopic classification is still an
open problem, vis--à--vis the paucity and (lack of) quality of the
best available data .
.
0.3truecm
Table I
0.3truecm
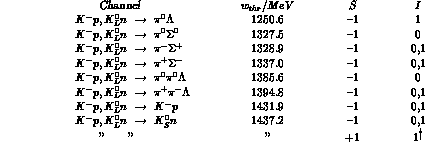
 ) This amplitude only appears in the regeneration process
) This amplitude only appears in the regeneration process
 .
.
Table II
0.3truecm
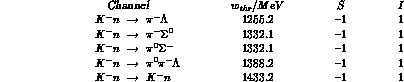
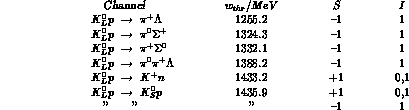
A formation experiment on bound nucleons in an (almost) 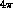 apparatus with good efficiency and resolution for low--momentum
apparatus with good efficiency and resolution for low--momentum 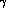 's
(such as KLOE) can reconstruct and measure a channel such as
's
(such as KLOE) can reconstruct and measure a channel such as 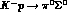 (only above the
(only above the 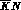 threshold) or
threshold) or 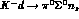 (both above and below threshold), which is pure
I = 0: up to now all analyses on the
(both above and below threshold), which is pure
I = 0: up to now all analyses on the 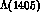 have been limited to
charged channels
have been limited to
charged channels , being thus forced to assume the I = 1 contamination
in their samples to be either negligible or smooth and not interfering with
the resonance signal (remember that it is common knowledge
, being thus forced to assume the I = 1 contamination
in their samples to be either negligible or smooth and not interfering with
the resonance signal (remember that it is common knowledge that there is a
P--wave resonance in the I = 1,
that there is a
P--wave resonance in the I = 1, 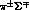 channels at 1384
MeV!). This situation is particularly unsatisfactory, in view of the fact
that the various spectroscopic models proposed for the classification of the
channels at 1384
MeV!). This situation is particularly unsatisfactory, in view of the fact
that the various spectroscopic models proposed for the classification of the
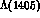 differ mostly in the detailed resonance shape, rather
than in its couplings
differ mostly in the detailed resonance shape, rather
than in its couplings : now, it is precisely the shape which could be
drastically changed even by a moderate amount of interference with an I = 1
``background''. Note also that, having in the same apparatus, and at almost
the same energy tagged
: now, it is precisely the shape which could be
drastically changed even by a moderate amount of interference with an I = 1
``background''. Note also that, having in the same apparatus, and at almost
the same energy tagged 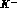 and
and 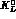 produced at the same point, one
can separate I=0 and I=1 channels with a minimum of systematic
uncertainties, by measuring all channels
produced at the same point, one
can separate I=0 and I=1 channels with a minimum of systematic
uncertainties, by measuring all channels 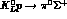 ,
,
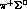 and
and 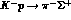 ,
, 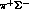 , besides, of
course, the above--mentioned, pure I=0,
, besides, of
course, the above--mentioned, pure I=0, 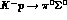 one.
one.
Another class of inelastic processes, which are expected to be produced
(even if at a much smaller rate) by DA NE's
NE's 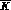 's, is
radiative capture, leading in hydrogen to the final states
's, is
radiative capture, leading in hydrogen to the final states 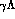 and
and 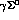 for incident
for incident 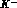 's, and, for incident
's, and, for incident 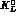 's, to the
final state
's, to the
final state 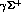 : in deuterium, one expects to observe the capture
processes by neutrons,
: in deuterium, one expects to observe the capture
processes by neutrons, 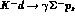 and
and 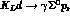 ,
, 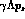 as well. Observation of these
processes has been limited up to now to searches for photons emitted after
capture of
as well. Observation of these
processes has been limited up to now to searches for photons emitted after
capture of 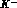 's stopped in liquid hydrogen (and deuterium): but in these
experiments the spectra are dominated by photons from unreconstructed
's stopped in liquid hydrogen (and deuterium): but in these
experiments the spectra are dominated by photons from unreconstructed 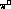 and
and 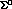 decays
decays . This poses serious difficulties already at the
level of separation of signals from background, since (in
. This poses serious difficulties already at the
level of separation of signals from background, since (in 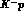 capture at
rest) only the photon line from the
capture at
rest) only the photon line from the 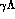 final state falls
just above the endpoint of the photons from decays of the
final state falls
just above the endpoint of the photons from decays of the 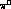 's in the
's in the
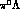 final state, while that from
final state, while that from 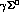 falls right on
top of this latter: indeed, these experiments were able to produce, within
quite large errors, only an estimate of the respective branching ratios.
falls right on
top of this latter: indeed, these experiments were able to produce, within
quite large errors, only an estimate of the respective branching ratios.
The 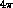 geometry possible at DA
geometry possible at DA NE, combined with the ``transparency''
of a KLOE--like apparatus, its high efficiency for photon detection and its
good resolution for spatial reconstruction of the events, should make possible
the full identification of the final states and therefore the measurement of
the absolute cross sections for these processes, although in flight and not
at rest.
NE, combined with the ``transparency''
of a KLOE--like apparatus, its high efficiency for photon detection and its
good resolution for spatial reconstruction of the events, should make possible
the full identification of the final states and therefore the measurement of
the absolute cross sections for these processes, although in flight and not
at rest.
This difference can be appreciated when comparing with theoretical
predictions: the main contributions to radiative captures are commonly
thought to come from radiative decays of resonant levels in the
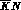 system
system , while the total hyperon production cross
section is expected to come from both resonant and non--resonant intermediate
states. An estimate of the branching ratios would therefore be quite sensitive
to the latter, while a prediction of the absolute cross sections should not.
, while the total hyperon production cross
section is expected to come from both resonant and non--resonant intermediate
states. An estimate of the branching ratios would therefore be quite sensitive
to the latter, while a prediction of the absolute cross sections should not.
Data are presently indicating branching ratios around
are presently indicating branching ratios around 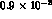 for
for 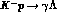 and
and 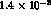 for
for 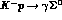 , with errors of the order of 15% on both rates: most
theoretical models
, with errors of the order of 15% on both rates: most
theoretical models tend to give the first rate larger than the
second, with both values consistently higher than the observed ones. Only a
cloudy--bag--model estimate
tend to give the first rate larger than the
second, with both values consistently higher than the observed ones. Only a
cloudy--bag--model estimate exhibits the trend appearing (although
only at a
exhibits the trend appearing (although
only at a 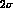 level, and therefore waiting for confirmation by better
data) from the first experimental determinations, but this is the only respect
in which this model agrees with the data, still giving branching ratios larger
than observations by a factor two
level, and therefore waiting for confirmation by better
data) from the first experimental determinations, but this is the only respect
in which this model agrees with the data, still giving branching ratios larger
than observations by a factor two .
.
Data are also interpretable in terms of 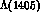 electromagnetic
transition moments
electromagnetic
transition moments : this interpretation of measurements taken at a
single energy, or over a limited interval, is clearly subject to the effect
of the interference between this state and all other contributions, such as
the
: this interpretation of measurements taken at a
single energy, or over a limited interval, is clearly subject to the effect
of the interference between this state and all other contributions, such as
the  -- and
-- and  --hyperon poles and other resonant states such
as the
--hyperon poles and other resonant states such
as the 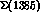 and the
and the 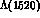 , not to mention t--channel
exchanges (since at least K--exchange has to be included, to ensure gauge
invariance of the Born approximation). An extraction of the
, not to mention t--channel
exchanges (since at least K--exchange has to be included, to ensure gauge
invariance of the Born approximation). An extraction of the 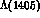 moments, relatively freer of these uncertainties, requires measurements of
the final states
moments, relatively freer of these uncertainties, requires measurements of
the final states 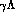 and
and 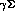 (if possible, in
different charge states) over the unphysical region, using (gaseous)
deuterium or helium as a ``target''. Rates are expected to be only of the
order of
(if possible, in
different charge states) over the unphysical region, using (gaseous)
deuterium or helium as a ``target''. Rates are expected to be only of the
order of  , but it must be kept in mind that such a low rate
(by DA
, but it must be kept in mind that such a low rate
(by DA NE's standards) corresponds already to statistics two orders
of magnitude above those of the best experiment performed till now on
the shape of the
NE's standards) corresponds already to statistics two orders
of magnitude above those of the best experiment performed till now on
the shape of the 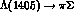 decay spectrum
decay spectrum .
.
1.0truecm 5. The K-matrix (or M-matrix) formalism. 0.3truecm
An adequate description of the low--energy 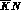 partial waves must
couple at least the dominant, two--body inelastic channels to each other and
to the elastic one; the three--body channel
partial waves must
couple at least the dominant, two--body inelastic channels to each other and
to the elastic one; the three--body channel 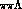 is expected to be
suppressed, for
is expected to be
suppressed, for 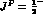 , by the angular momentum barrier, but it
could contribute appreciably to the I=0,
, by the angular momentum barrier, but it
could contribute appreciably to the I=0, 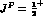 P--wave, due
to the strong final--state interaction of two pions in an I=0 S--wave.
Note that most bubble chamber experiments were unable to fully
reconstruct the events at the lowest momenta, and therefore often assumed all
directly produced
P--wave, due
to the strong final--state interaction of two pions in an I=0 S--wave.
Note that most bubble chamber experiments were unable to fully
reconstruct the events at the lowest momenta, and therefore often assumed all
directly produced  's to come from the
's to come from the 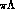 channel
alone, neglecting altogether the small
channel
alone, neglecting altogether the small 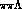 contribution.
contribution.
The appropriate formalism is to introduce a K--matrix description (sometimes it is convenient to use, instead of the K--matrix, its inverse, also known as the M--matrix), defined in the isospin eigenchannel notation as
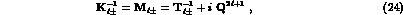
for both I=0, 1 S--waves (and perhaps also for the four P--waves as
well, or at least for the I=1, 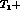 wave, which resonates below
threshold). The K--matrices, assuming
wave, which resonates below
threshold). The K--matrices, assuming 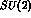 symmetry, describe the
S--wave data
at a given energy in terms of nine real parameters (six for I=1 and
three for I=0), while the experimentally accessible processes can be
described, assuming pure S--waves in the same symmetry limit, by only
six independent parameters, which can be chosen to be the two (complex)
amplitudes
symmetry, describe the
S--wave data
at a given energy in terms of nine real parameters (six for I=1 and
three for I=0), while the experimentally accessible processes can be
described, assuming pure S--waves in the same symmetry limit, by only
six independent parameters, which can be chosen to be the two (complex)
amplitudes  for the
for the 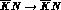 channel, the
phase difference
channel, the
phase difference  between the I=0 and I=1
between the I=0 and I=1 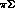 production
amplitudes, and the ratio
production
amplitudes, and the ratio  between the
between the 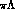 production cross
section and that for total hyperon production in an I=1 state
production cross
section and that for total hyperon production in an I=1 state .
.
Thus a single--energy measurement does not allow a complete determination of the K--matrix elements at that energy. Using high--statistics measurements at different momenta, and assuming either constant K--matrices or (if more complexity were needed) effective--range M--matrices could in principle fully determine the matrix elements: but for this to be possible one has to be able to subtract out the (small) P--wave contributions to the integrated cross sections
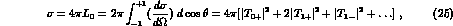
which could be obtained either from 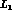 alone, for the elastic and
charge--exchange channels, or from both
alone, for the elastic and
charge--exchange channels, or from both 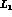 and
and 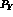 , which give
complementary information, for the hyperon production channels. None of these
quantities has been measured with the desirable accuracy up to now:
the TST Collaboration tried to extract
, which give
complementary information, for the hyperon production channels. None of these
quantities has been measured with the desirable accuracy up to now:
the TST Collaboration tried to extract
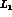 from some of their low--statistics data, and found results consistent
with the tail of the
from some of their low--statistics data, and found results consistent
with the tail of the 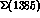 resonance in the I=1,
resonance in the I=1, 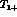 wave, but
also consistent (at the
wave, but
also consistent (at the 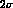 level) with zero within their obviously very
large errors
level) with zero within their obviously very
large errors . At the same level of accuracy, one should also be able to
isolate and separate out the
. At the same level of accuracy, one should also be able to
isolate and separate out the 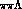 channel contribution as well.
channel contribution as well.
Remember that an accurate analysis has also to include the complete e.m.
corrections: up to now all 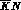 analyses have relied on the
formula derived by Dalitz and Tuan
analyses have relied on the
formula derived by Dalitz and Tuan for a pure S--wave
scattering with a weak hadronic, short--range interaction, which is hardly the
case for the
for a pure S--wave
scattering with a weak hadronic, short--range interaction, which is hardly the
case for the 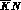 system around threshold.
system around threshold.
To fix the redundant K--matrix parameters, different authors have tried
different methods: some have used the data on the shape of the 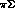 spectrum from production experiments
spectrum from production experiments , others have constrained the
amplitudes in the unphysical region by imposing consistency with dispersion
relations for the amplitudes D for both
, others have constrained the
amplitudes in the unphysical region by imposing consistency with dispersion
relations for the amplitudes D for both 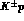 and
and 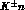 forward
elastic scattering
forward
elastic scattering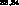 , relying on the existence of accurate data on the
total cross sections at higher energies. More recently, some attempts have
been made to combine both constraints into a ``global'' analysis, but with no
better results than each of them taken separately
, relying on the existence of accurate data on the
total cross sections at higher energies. More recently, some attempts have
been made to combine both constraints into a ``global'' analysis, but with no
better results than each of them taken separately .
.
Unfortunately, neither of these methods has been very powerful, because of the
low statistics of the 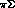 production data on one side, and on the
other because of the need to use for the dispersion relations the often not
very accurate information (and particularly so for the
production data on one side, and on the
other because of the need to use for the dispersion relations the often not
very accurate information (and particularly so for the 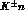 amplitudes)
on the real--to--imaginary--part ratios.
amplitudes)
on the real--to--imaginary--part ratios.
We list below (without errors, often meaningless since the parameters are
strongly correlated, and therefore not even quoted by some of the authors) the
constant K--matrices found by Chao et al. using the first method (which did not include the TST Collaboration data), and the more complex
parametrization found by A.D. Martin using the second
(which did not include the TST Collaboration data), and the more complex
parametrization found by A.D. Martin using the second (and including
the preliminary TST data). Note that to describe the data for I=0 both
above and below threshold A.D. Martin was forced to introduce a
``constant--effective--range'' M--matrix, where
(and including
the preliminary TST data). Note that to describe the data for I=0 both
above and below threshold A.D. Martin was forced to introduce a
``constant--effective--range'' M--matrix, where 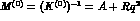 , with three more ``effective range''
parameters, so that to make the two analyses comparable we list separately his
threshold K--matrix values.
, with three more ``effective range''
parameters, so that to make the two analyses comparable we list separately his
threshold K--matrix values.
The purpose of this table is to show that there is considerable uncertainty
even on the value of the 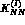 elements of the K--matrices (the real
parts of the corresponding scattering lengths): the data have been
re--analyzed by Dalitz et al.
elements of the K--matrices (the real
parts of the corresponding scattering lengths): the data have been
re--analyzed by Dalitz et al. , using both sets of
constraints with different weigths and different parametrizations, and
yielding a variety of fits, all of them of about the same overall quality and
none of them improving very much over the above ones.
, using both sets of
constraints with different weigths and different parametrizations, and
yielding a variety of fits, all of them of about the same overall quality and
none of them improving very much over the above ones.
Just to highlight the difficulties met in describing the data (probably
plagued by inconsistencies between different experiments, and by
large systematic uncertainties), we point out
that A.D. Martin himself found that including in his analysis a
found that including in his analysis a
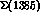 resonance at the right position, with the width given by
the production experiments (and listed in the Particle Data Group tables
resonance at the right position, with the width given by
the production experiments (and listed in the Particle Data Group tables )
and the coupling to the
)
and the coupling to the 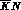 channel dictated by flavour--
channel dictated by flavour--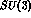 symmetry, was worsening rather than improving the fits obtained
neglecting it altogether: his analysis therefore considers
the
symmetry, was worsening rather than improving the fits obtained
neglecting it altogether: his analysis therefore considers
the  Born--term contribution a ``superposition'' of the former and
of that of the P--wave resonance, a rather unsavoury situation considering
the different
Born--term contribution a ``superposition'' of the former and
of that of the P--wave resonance, a rather unsavoury situation considering
the different 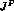 quantum numbers of the two states, which may raise
questions about the applicability of his analysis away from
quantum numbers of the two states, which may raise
questions about the applicability of his analysis away from 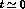 .
Note that a similar superposition
has to be considered in the
.
Note that a similar superposition
has to be considered in the 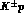 dispersion relations for the
dispersion relations for the  --
and
--
and  --pole contributions, which can not be separated from each other
due to their being very close in the
--pole contributions, which can not be separated from each other
due to their being very close in the  --variable plane:
here however the two states contribute to the same partial wave, and the
--variable plane:
here however the two states contribute to the same partial wave, and the
 --pole can be independently extracted from
--pole can be independently extracted from 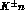 scattering
(or
scattering
(or 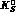 regeneration on protons) data
regeneration on protons) data .
.
In the analysis of the low--energy data collected
in the past on these processes, one of the main difficulties
comes from the large spread in momentum of the
typical low--energy kaon beams, for 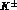 's because of the degrading in a
``moderator'' of the higher--energy beams needed to transport the kaons
away from their production target, for
's because of the degrading in a
``moderator'' of the higher--energy beams needed to transport the kaons
away from their production target, for 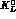 's because of the large
apertures needed to
achieve satisfactory rates in the targets (typically bubble chambers): this
made unrealistic the proposals (advanced from the early seventies) of better
determining the low--energy
K--matrices by studying the behaviour of the cross sections for
's because of the large
apertures needed to
achieve satisfactory rates in the targets (typically bubble chambers): this
made unrealistic the proposals (advanced from the early seventies) of better
determining the low--energy
K--matrices by studying the behaviour of the cross sections for
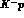 --initiated processes at the
--initiated processes at the
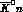 charge--exchange threshold
charge--exchange threshold .
The high momentum resolution
available at DA
.
The high momentum resolution
available at DA NE will instead make such a goal a realistically
achievable one.
0.8truecm
Table IV
0.3truecm
NE will instead make such a goal a realistically
achievable one.
0.8truecm
Table IV
0.3truecm
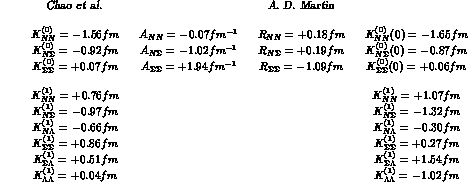
In this case one can no longer assume
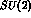 to be a good symmetry of the amplitudes: under the (reasonable)
assumption that the forces are still
to be a good symmetry of the amplitudes: under the (reasonable)
assumption that the forces are still 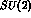 --symmetric, one can however
still retain the previous K--matrix formalism, but one can no longer
decouple the different isospin eigenchannels
--symmetric, one can however
still retain the previous K--matrix formalism, but one can no longer
decouple the different isospin eigenchannels .
Introducing the orthogonal matrix R, which
transforms the six isospin eigenchannels for
.
Introducing the orthogonal matrix R, which
transforms the six isospin eigenchannels for 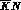 (I=0, 1),
(I=0, 1),
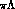 (I=1 only) and
(I=1 only) and 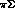 (I=0, 1, 2) into the
six physical charge channels
(I=0, 1, 2) into the
six physical charge channels 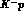 ,
, 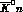 ,
, 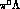 ,
,
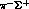 ,
,  and
and 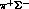 , and the diagonal matrix
Q
, and the diagonal matrix
Q of the c.m. momenta for these latter, one can rewrite
the T--matrix for the S--waves in the isospin--eigenchannel space as
of the c.m. momenta for these latter, one can rewrite
the T--matrix for the S--waves in the isospin--eigenchannel space as
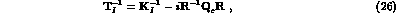
where K is a box matrix with zero elements between channels of
different isospin, and R
is a box matrix with zero elements between channels of
different isospin, and R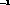 Q
Q R is of course no
longer diagonal.
R is of course no
longer diagonal.
Apparently this involves one more parameter, since it
also contains the element 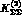 : in practice, if one is
interested in the behaviour of the cross sections in the neighbourhood of
the
: in practice, if one is
interested in the behaviour of the cross sections in the neighbourhood of
the 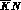 charge--exchange threshold, one can take the
c.m. momenta in the three
charge--exchange threshold, one can take the
c.m. momenta in the three 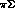 channels as equal, so that the
I=2,
channels as equal, so that the
I=2, 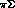 channel
decouples from the
channel
decouples from the 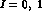 ones, since the ``rotated'' matrix
R
ones, since the ``rotated'' matrix
R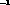 Q
Q R
has now only two non--zero, off-diagonal elements, equal to
R
has now only two non--zero, off-diagonal elements, equal to
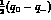 (where the subscripts refer to the kaon charges),
between the I=0 and I=1
(where the subscripts refer to the kaon charges),
between the I=0 and I=1 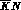 channels,
the diagonal ones being almost the
same as in the fully
channels,
the diagonal ones being almost the
same as in the fully 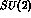 --symmetric case, with only the substitution
to the
--symmetric case, with only the substitution
to the 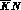 channel momentum q of the average over the two charge
states,
channel momentum q of the average over the two charge
states, 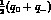 .
. 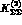 would however be
important for describing accurate experiments on
would however be
important for describing accurate experiments on 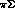 and
and 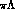 mass spectra in the unphysical region below the
mass spectra in the unphysical region below the 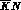 threshold
without recourse to an
threshold
without recourse to an 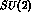 --symmetry limit: but the state--of--the--art
of our understanding of wave--functions, even for the lightest nuclei, is not
such as to make these isotopic--symmetry--breaking corrections relevant.
--symmetry limit: but the state--of--the--art
of our understanding of wave--functions, even for the lightest nuclei, is not
such as to make these isotopic--symmetry--breaking corrections relevant.
1.0truecm
5. Low--energy 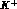 scattering is important, too.
0.3truecm
scattering is important, too.
0.3truecm
Better information on the S=+1 system is also essential in several cases. We
limit ourselves to mention only two of the problems coming to our mind.
Isospin symmetry, as can be seen from the previous section, is an
essential ingredient in the phenomenological analysis of the KN system,
apart from obvious mass--difference effects, apparent only in the close
proximity of the thresholds, which one can describe by modifying the
K--matrix formalism as outlined above .
.
One way to check isospin symmetry is to relate the amplitudes derived from
charged kaon scattering to the data from 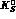 regeneration. Since isospin relates the scattering of charged kaons on protons
to the regeneration on neutrons (and vice versa), the test is better
performed on an isoscalar nuclear target, such as deuterium or
regeneration. Since isospin relates the scattering of charged kaons on protons
to the regeneration on neutrons (and vice versa), the test is better
performed on an isoscalar nuclear target, such as deuterium or  He. We
should have indeed, apart from kinematical corrections and CP--violation
effects,
He. We
should have indeed, apart from kinematical corrections and CP--violation
effects,
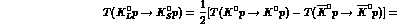
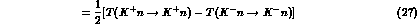
and
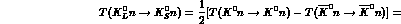
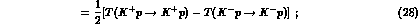
when we introduce these equalities in a nuclear scattering calculation, as in
e.g. a Glauber model, all elastic multiple scattering effects
should apply equally to both the right-- and left--hand sides of the
equalities for an isoscalar nucleus, protecting the identity from a large
fraction of the ``nuclear'' effects .
.
Up to now such tests would have been possible only at higher momenta, where the opening of inelastic channels in the S=+1 systems complicates calculations further: a test performed in the elastic region of this system should make things simpler and clearer, at least in the S=+1 sector.
The second problem, related in many theoretical analyses to observations from
inelastic electron and muon scattering on nuclei, namely to changes in the
electromagnetic properties and in the deep--inelastic structure functions of
nucleons bound in nuclei with respect to the free ones, is the
``antishadowing'' effect observed at momenta around 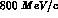 for
for 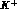 scattering on nuclear targets
scattering on nuclear targets .
Conventional Glauber--model calculations
.
Conventional Glauber--model calculations led to
expect a ratio
led to
expect a ratio 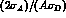 slightly less than unity and
decreasing with both the kaon momentum and the target mass number A,
while the measured
values were larger than unity and increasing with momentum.
This led to think,
as an explanation of this and of the aforementioned
electromagnetic phenomena, of
a ``swelling'' of the bound nucleons with respect to free ones, in line with
some of the explanations put forward for the ``nuclear'' EMC effect, though at
a much higher energy scale
slightly less than unity and
decreasing with both the kaon momentum and the target mass number A,
while the measured
values were larger than unity and increasing with momentum.
This led to think,
as an explanation of this and of the aforementioned
electromagnetic phenomena, of
a ``swelling'' of the bound nucleons with respect to free ones, in line with
some of the explanations put forward for the ``nuclear'' EMC effect, though at
a much higher energy scale .
.
New data have recently confirmed this trend ,
but only for momenta higher than approximately
,
but only for momenta higher than approximately 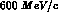 ; a
possibility coming to mind is that the opening of inelastic channels, such as
; a
possibility coming to mind is that the opening of inelastic channels, such as
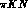 (or more simply quasi--two--body ones as
(or more simply quasi--two--body ones as  and
and 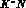 ),
might necessitate the
introduction of inelastic intermediate states absent in a conventional
Glauber--model calculation, phenomenon analogous to the need to introduce
inelastic diffraction in the intermediate steps of a multiple--scattering
formalism to explain diffractive
processes on nuclei at much higher energies:
thus the data would be just showing the opening of the
threshold for such a phenomenon, particularly visible in the
),
might necessitate the
introduction of inelastic intermediate states absent in a conventional
Glauber--model calculation, phenomenon analogous to the need to introduce
inelastic diffraction in the intermediate steps of a multiple--scattering
formalism to explain diffractive
processes on nuclei at much higher energies:
thus the data would be just showing the opening of the
threshold for such a phenomenon, particularly visible in the 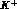 --scattering
case because of the extremely long mean--free path of this hadron in nuclear
matter (about
--scattering
case because of the extremely long mean--free path of this hadron in nuclear
matter (about 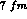 ).
).
Measurements of the 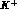 cross sections on different nuclei in DA
cross sections on different nuclei in DA NE's
kinematical region, where
NE's
kinematical region, where 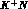 interactions are purely elastic, should help
close the issue when compared with accurate Glauber--model
calculations
interactions are purely elastic, should help
close the issue when compared with accurate Glauber--model
calculations .
.
We would like to close reminding the reader that information on the 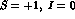 channel in this energy region is coming entirely from
extrapolations from higher--momen-tum data, since
channel in this energy region is coming entirely from
extrapolations from higher--momen-tum data, since 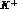 --scattering (and
regeneration) data on deuterium are not available at momenta lower than
about
--scattering (and
regeneration) data on deuterium are not available at momenta lower than
about 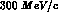 : at present we have only a generic idea about the order of
magnitude of the absolute value of the KN I=0 scattering length,
expected to be of the order of some times
: at present we have only a generic idea about the order of
magnitude of the absolute value of the KN I=0 scattering length,
expected to be of the order of some times 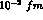 from forward
dispersion relations and the lowest--momentum regeneration data
from forward
dispersion relations and the lowest--momentum regeneration data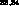 .
An accurate measurement of the cross sections for
.
An accurate measurement of the cross sections for 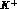 incoherent
scattering on deuterium, possible at
DA
incoherent
scattering on deuterium, possible at
DA NE over a wide angular range, would thus give us the first
direct measurement of this quantity.
NE over a wide angular range, would thus give us the first
direct measurement of this quantity.
2.0truecm
REFERENCES AND FOOTNOTES
0.3truecm
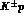 data: W.E. Humphrey and R.R. Ross: Phys. Rev.
127 (1962) 1; G.S. Abrams and B. Sechi--Zorn: Phys. Rev. 139
(1965) B 454; M. Sakitt, et al.: Phys Rev 139 (1965) B 719; J.K.
Kim: Columbia Univ. report NEVIS--149 (1966), and Phys. Rev. Lett.
14 (1970) 615; W. Kittel, G Otter and I. Wacek: Phys. Lett
21 (1966) 349; D. Tovee, et al.: Nucl. Phys. B 33 (1971)
493; T.S. Mast, et al.: Phys. Rev. D 11 (1975) 3078, and D
14 (1976) 13; R.O. Bargenter, et al.: Phys. Rev. D 23 (1981)
1484.
data: W.E. Humphrey and R.R. Ross: Phys. Rev.
127 (1962) 1; G.S. Abrams and B. Sechi--Zorn: Phys. Rev. 139
(1965) B 454; M. Sakitt, et al.: Phys Rev 139 (1965) B 719; J.K.
Kim: Columbia Univ. report NEVIS--149 (1966), and Phys. Rev. Lett.
14 (1970) 615; W. Kittel, G Otter and I. Wacek: Phys. Lett
21 (1966) 349; D. Tovee, et al.: Nucl. Phys. B 33 (1971)
493; T.S. Mast, et al.: Phys. Rev. D 11 (1975) 3078, and D
14 (1976) 13; R.O. Bargenter, et al.: Phys. Rev. D 23 (1981)
1484. 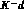 data: R. Armenteros, et al.: Nucl. Phys. B 18 (1970)
425.
data: R. Armenteros, et al.: Nucl. Phys. B 18 (1970)
425.
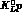 data: J.A. Kadyk, et al.: Phys. Lett. 17 (1966)
599, and report UCRL--18325 (1968); R.A. Donald, et al.: Phys.
Lett. 22 (1966) 711; G.A. Sayer, et al.: Phys. Rev. 169
(1968) 1045.
data: J.A. Kadyk, et al.: Phys. Lett. 17 (1966)
599, and report UCRL--18325 (1968); R.A. Donald, et al.: Phys.
Lett. 22 (1966) 711; G.A. Sayer, et al.: Phys. Rev. 169
(1968) 1045.
 scattering.
scattering.