- Scientific case -
The Pauli Exclusion Principle (PEP) represents one of the fundamental principles of the modern physics and all our comprehension of the surrounding matter is based on it. Even if today there are no compelling reasons to doubt its validity, it still spurs a lively debate on its limits, as testified by the abundant contributions found in the literature and in topical conferences [3].
Before discussing the present status of the Pauli Exclusion Principle, let’s briefly summarize PEP in non-relativistic quantum mechanics (following Mandl [4]).
Consider, for example, the helium atom Hamiltonian:
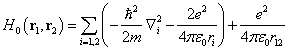
which is symmetric with respect to the coordinate exchange of the two electrons. Requiring the Hamiltonian to be symmetric corresponds to assume that the two electrons are indistinguishable. Even in the case of an approximate, non-relativistic, Hamiltonian, the indistinguishable character of the two electrons tells us the fact that the exact Hamiltonian should contain the same type of symmetry. For example, if one includes the spin s, the Hamiltonian should be a function of the type 
and should continue to be symmetric with respect to the 1-2 exchange operation.
Generally, considering the Hamiltonian of a system of N electrons, the indistinguishability constrains us to write it such as to be invariant to the any-two i,j electron exchange operation:
The symmetry of the Hamiltonian induces a degeneration of the eigenvalues, namely:
.
One can therefore define the following linear combinations:
which are the eigenfunctions for the same eigenvalue having a defined parity (±1) with respect to the 1-2 permutation.
Furthermore, one can deduce that the time evolution dictated by the Schroedinger equation:
cannot modify the symmetry of the wave-functions (the Hamiltonian commutes with the permutations).
In the case of 3 or more particles the situation is a bit more complex. Let’s consider, for example, the linear combination:
which for the 1-2 exchange becomes the new linear combination:
,
which has no common term with the initial combination, or with the:
one, which contains terms with all possible permutations, but, when 1-2 exchange is done, becomes:
which obviously has no defined parity. Generalizing these considerations, one can see that the group of the linear combinations:
is closed with respect to the group of the 1,2,3 symbol permutations, and, moreover, there exists a subgroup constituted by only one linear completely symmetric combination:
which transforms in itself. The same happens to the completely antisymmetric linear combination:
The symmetrization postulate states that the only acceptable (“physical”) linear combinations are either completely symmetric or antisymmetric, condition which adds to the symmetry of the Hamiltonian (which is dictated by the indistinguishability of particles). In 1940 W. Pauli demonstrated that a relativistic field theory for identical particles can be built only if the integer-spin particles do have symmetric wave functions while the half-integer spin ones have antisymmetric wave functions [5]. At this point, it is important to notice that in the case of non-interacting particles one can write the global wave function in terms of superposition of the single-particle ones.
For example, in the case of 2 particles of half-integer spin, one can write the wave-function as:
where a, b are the spin indices. If the particle spins are equal, then:
the wave function is identically zero, i.e. unphysical state, meaning that two particles with half-integer spin cannot be in the same quantum state: in this form they symmetrization principle is known as the Pauli Exclusion Principle.
As one can check, in the exclusion principle there are actually two assumptions: particles of the same “type” are indistinguishable, and the global wave function is antisymmetric. Moreover, it contains a relativistic element, namely the particle spin coordinate.
It is worthy to note that Dirac [6] and Pauli [7] considered in depth the consequences of this principle and concluded that the electronic transitions towards a free shell of an atom could be forbidden by the symmetrization alone, independently of the exclusion principle validity, because such transitions would modify the symmetry of the wave function.
Moving now to relativistic quantum mechanics, it is rather easy to demonstrate that the second quantization of the Dirac’s equation retains physical meaning only if the corresponding fields do anticommute [8], while the Klein-Gordon equation is valid for commuting fields [8]. It is however less easy to prove that, generally, a quantum theory is coherent only if the half-integer spin particles are described by anticommutators while the integer spin ones by commutators.
As previously mentioned, Pauli gave a first rigorous demonstration of this link between spin and statistics in 1940 in a classic paper [5]. In the following years, other physicists investigated the link between spin and statistics, and, one of the clearest formulations is the one of Lüders and Zumino [9].
In their paper they consider a theory obeying to the following postulates:
1. invariance with respect to the proper inhomogeoneus Lorentz group (including translations, but not reflections);
2. any two operators applied on the same field at points separated by a space-like interval, can either commute or anticommute (locality hypothesis);
3. the vacuum represents the minimum energy state;
4. Hilbert space metric is positively defined;
5. the vacuum state it is not identically destroyed by a field operator.
From these hypotheses they demonstrate that pseudoscalar (spin 0) fields commute while spin 
fields anticommute.
An important added value of Lüders and Zumino work is the fact that it is valid for interacting particles as well.
The Pauli principle plays a fundamental role in the explanation of several physical processes, ranging from the atomic periodic table, to the theory of electric conduction in metals, to the degeneracy pressure which makes both white dwarfs and neutron stars stable.
Although the principle is spectacularly confirmed by the number and the accuracy of its predictions, it is still possible to speculate that it is only an approximation of a more fundamental law, and that there may be tiny violations.
It is not trivial to build a theory which consistently incorporates a violation of the Pauli Exclusion Principle, and it is surely beyong the scope of this introduction to account for all the more or less successful attempts. Just to give a flavour of such a theory, we present a simple case, namely the Ignatiev and Kuzmin (IK) model [10]. In this model, creation and destruction operators connect 3 states, the vacuum state 
, the single occupancy state 
and a nonstandard double occupancy state 
, through the following relations:
from which the algebra of the operators is obtained as:
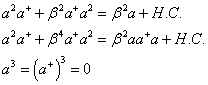
(this represents a particular case of the trilinear algebra introduced by Green [11]). Successively, one introduces the particles number operator N, which obeys at the well known commutation relations:
and one finds that this operator can be expressed as a function of the creation and destruction operators as:
(I being the identity operator). The IK paper concludes with a detailed exam of a perturbed Hamiltonian which includes an explicit violation of the exclusion principle and from here one calculates a transition probability per unit time 
, which obviously depends of the violation parameter b.
Applying this model to the electrons one can interpret the states and as states occupied by one or more electrons. Experimentally this means that anomalous atoms could exist (atoms with an anomalous filling of the electron shells) and/or that instability conditions could emerge (an electron can pass from to through the emission of an X-ray). This is the very reason which motivated past searches for anomalous X-rays and for the so-called non-Paulian atoms.
The IK theory introduces, in a simple and seemingly natural way, the violation of the Pauli principle. Many objections can be raised against this theory, as those formulated in a paper by Amado and Primakoff [12] who state that:
1. if the Hamiltonian is symmetric, then transitions to a state with a different permutation symmetry are not allowed;
2. if the electrons can have an antisymmetric component, then, due to the indistinguishability of electrons, all electrons should be “a bit” antisymmetric. On the other hand, this “bit” should not be necessarily small, and then one can wonder why, in reality, should then be so “extremely small”.;
3. if different symmetry states do exist, than the components having different symmetry should be degenerate in energy and this close to a “miracle”, since it is exceedingly unlikely that such a coincidence takes place;
4. a way out could be to give up to the perfect indistinguishability and to assume that particles very similar, but not identical, do exist. But – if all electrons could be, even very slightly different, the exclusion principle would not hold in many cases and this is in contrast with the experimental evidence;
5. another possibility is that only some electrons are different, but in such a case the radiative transitions to the K shell should have occurred long time ago, and then it is not very likely that one can presently observe X rays from this process. Moreover, this hypothesis would give rise to an increase (not observed) of the experimental cross-section in the e+e- colliders.
Apart of the Amado and Primakoff observations, there are some more technical ones, as the one of Biedenharn, Truini and van Dam (BTvD), who directly criticize the IK model [13]. BTvD introduce two states, called 
and 
, and creation and destruction operators which act on the tensorial product of the states according to the relations:
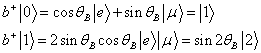
If now one replaces 
, same relations as the IK ones are obtained, meaning that the IK model is nothing else than a formulation of a theory which contains two similar fermions which mix, but remain different one from the other.
These, however, are very subtle arguments and it is easy to get wrong answers: Okun, in one of his famous articles [14], notes that the BTvD argument is not valid, unless the states are degenerate in mass, and such states are excluded by experiments. Unfortunately the IK model leads to negative probability states as remarked by Govorkov [15] and this destroys quite a bit its credibility.
It is clear that part of the interest towards these very important fundamental principles is due to their evasiveness, thing which is well expressed in a small note on American Journal of Physics in 1994 [16], in which D. E. Neuenschwander asked if there were progress towards an elementary explanation of the spin-statistics theorem, which even R. Feynman was unable to give.
Feynman wrote [17]:
This brings up an interesting question: Why is it that particles with half-integral spin are Fermi particles (...) whereas particles with integral spin are Bose particles (...)?
We apologize for the fact that we can not give you an elementary explanation.
An explanation has been worked out by Pauli from complicated arguments from quantum field theory and relativity. He has shown that the two must necessarily go together, but we have not been able to find a way to reproduce his arguments on an elementary level. It appears to be one of the few places in physics where there is a rule which can be stated very simply, but for which no one has found a simple and easy explanation. (...)
This probably means that we do not have a complete understanding of the fundamental principle involved. For the moment, you will just have to take it as one of the rules of the world.
Just as an answer to Neuenschwander’s question, in 1998 Duck and Sudarshan review paper [8] appeared; apart from this work, the theoretical situation is reviewed by Messiah and Greenberg (1966) [18], by Sudarshan (2000), and in the Streater’s and Wightman’s [19], as well as Duck’s e Sudarshan’s books [20].
It is important to mention here the works of Greenberg and collaborators [21-26], as well as the recent work of Berry and Robbins to understand the symmetrization principle based on geometrical transformations [27,28].
Greenberg and Mohapatra [22] in their work laid the basis of one of the recent experimental checks of the exclusion principle for electrons [2], which, in turn, has inspired the VIP proposal. In their work they put forward a hypothesis concerning the possible origin of an apparent Pauli exclusion principle violation: namely the possible existence of compactified extra-dimensions. In this case, the Pauli principle would remain perfectly valid in a space with more than 3+1 space-time dimensions.
Obviously, the indistinguishability and the symmetrization (or antisymmetrization) of the wave-function should be checked independently for each particle, and accurate tests were or are done for nucleons and photons, apart from electrons (the papers [29-41] represent a partial list of the experimental tests performed in recent years).
The VIP experiment aims to improve the current limit on the violation of the Pauli principle for electrons, (P<1.7 x 10-26), reported in [2], by four orders of magnitude (P< 10-30), exploring a region where new theories [8,22] allow for a possible PEP violation.