| For a continuous (periodic or quasi-periodic) signal
of amplitude 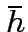 at
the frequency at
the frequency 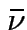 the
squared modulus of the Fourier Transform provides the
squared modulus of the Fourier Transform provides 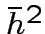 with
a noise contribution of with
a noise contribution of
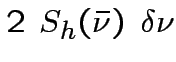 ,
being ,
being
 the
two-sided noise power spectrum of the detector (measured in 1/Hz). Thus
the SNR for periodic signals is: the
two-sided noise power spectrum of the detector (measured in 1/Hz). Thus
the SNR for periodic signals is:
The Eq. holds if the instantaneous frequency of the continuous
signal at the detector is known. The analysis procedure in this case is
``coherent'', since the phase information contained in the data is used
and the sensitivity (in amplitude) increases with the square-root of the
time. For periodic waves the sensitivity of a bar detector at its resonances
is given by:
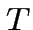 is the
bar temperature; is the
bar temperature; 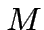 its
mass; its
mass; 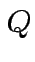 the
merit factor; the
merit factor; 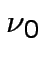 the
resonance frequency of the mode; the
resonance frequency of the mode; 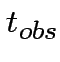 the
observation time.After one year of effective observation, the minimum
detectable the
observation time.After one year of effective observation, the minimum
detectable 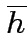 (amplitude
detectable with SNR=1), using the nominal parameters of the Explorer
detector ( (amplitude
detectable with SNR=1), using the nominal parameters of the Explorer
detector (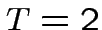 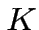 , ,
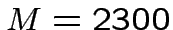 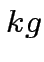 , ,
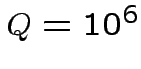 ),
is ),
is

For the NAUTILUS detectors, cooled at 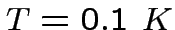 ,
the expected sensitivity is: ,
the expected sensitivity is:
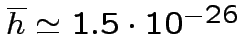 at
the resonances.In some cases it may be impossible, for various reasons,
to perform a single Fourier Transform over all the data. This means that
the observation time has to be divided in at
the resonances.In some cases it may be impossible, for various reasons,
to perform a single Fourier Transform over all the data. This means that
the observation time has to be divided in 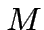 sub-periods,
such that the spectral resolution of the spectra becomes sub-periods,
such that the spectral resolution of the spectra becomes
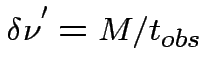 and
the corresponding and
the corresponding 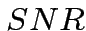 is is
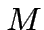 times smaller than that
given by Eq. 1. The times smaller than that
given by Eq. 1. The 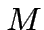 spectra
can be combined together, for example, by incoherent summation, that is
by averaging the square modulus, or using pattern-tracking procedures
(variuos papers have been done on this problem ) In this case the final
spectral resolution is again spectra
can be combined together, for example, by incoherent summation, that is
by averaging the square modulus, or using pattern-tracking procedures
(variuos papers have been done on this problem ) In this case the final
spectral resolution is again
 but there
is still some gain as the averaging reduces the variance of the noise
in each bin. We obtain: but there
is still some gain as the averaging reduces the variance of the noise
in each bin. We obtain:
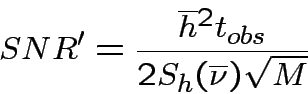
We have developed a procedure for the search of signals
from periodic sources in the data of gravitational wave detectors. We
have analyzed data of the resonant detector Explorer, searching for sources
located in the Galactic Center (GC). No signals with amplitude greater
than
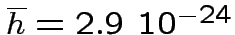 , in the
range 921.32-921.38 Hz, were observed using data collected over a time
period of 95.7 days, for a source located at , in the
range 921.32-921.38 Hz, were observed using data collected over a time
period of 95.7 days, for a source located at
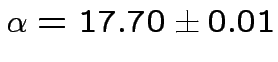 hours
and hours
and
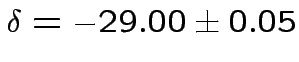 degrees.
The procedure we have used can be extended for any assumed position in
the sky and for a more general all-sky search, with the proper frequency
correction to account for the spin-down and Doppler effects. The results
are being printed on PRD (2001). degrees.
The procedure we have used can be extended for any assumed position in
the sky and for a more general all-sky search, with the proper frequency
correction to account for the spin-down and Doppler effects. The results
are being printed on PRD (2001). |

